Конструкции валов БМП.
Входные (быстроходные) валы имеют концевые участки, участки для установки подшипников, и участки, на которых нарезают зубья шестерён цилиндрических или конических зубчатых передач (Рис.5.3.)
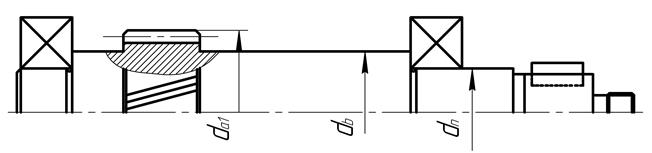
Рис 5.3
Конструкция быстроходного вала.
da1– диаметр шестерни, db– диаметр вала, dп–посадочный диаметр вала под подшипник
На входном валу цилиндрической передачи зубья шестерён нарезают на среднем участке. Диаметр его определён размером dбп , значение которого находится из условия надёжного контакта заплечика и внутреннего кольца подшипника (Рис.5.3). Конструкция вала на среднем участке зависит от передаточного числа и значения межосевого расстояния передачи. При небольших передаточных числах и относительно большом межосевом расстоянии диаметр df1 окружности впадин шестерни больше диаметра dбп вала; при больших передаточных числах и малом межосевом расстоянии df1 < dбп, ; при этом предусматривают участки для выхода фрезы, нарезающей зубья.
Промежуточные валы не имеют концевых участков. На самом валу нарезаны зубья шестерни тихоходной ступени. Рядом расположено колесо быстроходной ступени.
Выходные (тихоходные) валы имеют концевой участок (Рис.5.4).
В средней части вала между подшипниковыми опорами размещают зубчатое колесо. Наиболее типичная конструкция вала показана на рис.5.4.
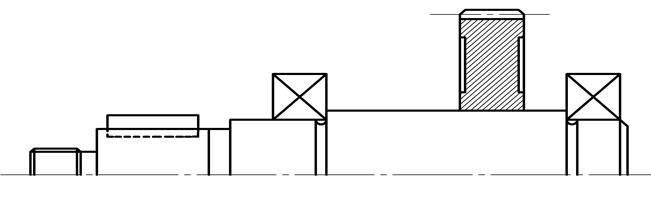
Рис.5.4.
Конструкция выходного (тихоходного) вала.
В сопряжении колеса с валом используется посадка с большим натягом. Подшипники установлены до упора в заплечики вала. Валы следует конструировать гладкими, с минимальным числом уступов, что позволяет существенно сократить расход металла на изготовление вала и упростить сборку колеса.
После определения диаметров и длин участков вала, а также его конструктивных элементов, производят расчёт вала на сопротивление усталости. Известно, что шпоночные пазы, резьбы под установочные гайки, отверстия под винты, канавки и резкие изменения сечений вала вызывают концентрацию напряжений, уменьшающую его усталостную прочность. Поэтому, если вал имеет небольшой запас по сопротивлению усталости, следует избегать использования элементов, вызывающих концентрацию напряжений.
5.2.2. Расчёты валов на прочность.
Основными нагрузками на валы являются силы и моменты от передач. Силы на валы передаются через насаженные на них детали: зубчатые или червячные колёса, шкивы и полумуфты. Под действием постоянных по значению и направлению сил во вращающихся валах возникают напряжения, меняющиеся по симметричному циклу [3].
Для изготовления большинства валов применяют термически обрабатываемые среднеуглеродистые и легированные стали: 45,40Х, 12 ХН3А. и другие.
Таблица 5.1
| Марка стали | Диаметр заготовки мм | Твёр-дость НВ (не менее) | Механические характеристики МПа | Коэффи-циент Ψт | ||||
| σв | σт | τт | σ-1 | τ-1 | ||||
| Ст5 | любой | 0,06 | ||||||
| ≤ 120 ≤ 80 | 0,09 1,10 | |||||||
| 40Х | ≤ 200 ≤ 120 | 0,09 0,10 | ||||||
| 40ХН | ≤ 200 | 0,10 | ||||||
| 20Х | ≤ 120 | 0,07 | ||||||
| 12ХН3А | ≤ 120 | 0,10 | ||||||
| 18ХГТ | ≤ 60 | 0,12 |
Выполняют расчёт валов на статическую прочность и на сопротивление усталости. Расчёт выполняют в такой последовательности. По чертежу вала в сборе составляют расчётную схему, на которую наносят все внешние силы, нагружающие вал, приводя плоскости их действия к двум взаимно-перпендикулярным плоскостям (горизонтальной X и вертикальной Y). Затем определяют реакции опор в горизонтальной и вертикальной плоскостях. В этих же плоскостях строят эпюры изгибающих моментов МХ и МY и отдельно эпюру крутящего момента МК, эпюру изгибающего момента МКОН от консольной силы FK, и эпюру осевой силы Fа. Затем определяют (приближённо) опасные сечения с учётом эпюр моментов, размеров сечений вала и концентраторов напряжений. Под концентраторами напряжений имеют в виду сечения, в которых приложены внешние силы, моменты, реакции опор или места изменения сечений вала, нагруженные моментами. Затем проверяют прочность вала в опасных сечениях.
Расчёт на статическую прочность.
Проверку статической прочности выполняют для предупреждения пластической деформации при действии кратковременных перегрузок (при пуске, разгоне, реверсировании, торможении и так далее.) Величина перегрузки зависит от вида привода. Так, при наличии предохранительной муфты, величину перегрузки определяет момент, при котором эта муфта срабатывает. При отсутствии предохранительной муфты перегрузку принимают равной перегрузе при пуске приводного электродвигателя.
В расчёте используется коэффициент перегрузки КП.
КП = Тmax ∕ Т , где Тmax максимальный кратковременный действующий вращающий момент; Т – номинальный (расчётный) вращающий момент. Для большинства асинхронных электродвигателей
КП =2,2 [2,3].
При расчёте определяют нормальные σ и касательные τ напряжения в рассматриваемом сечении вала при действии максимальных нагрузок:
σ = 103 Мmax /W + Fmax /A
τ = 103 MKmax /Wk (5.9)
где Мmax = Кп·(√ Мх2 + Мy2 +Мкон- суммарный изгибающий момент, Н·М.
MKmax = Тmax = Кп·Т – крутящий момент, Н·М.
Fmax = Kп·Fа - осевая сила, Н; Wи и Wк - моменты сопротивления сечения вала при расчёте на изгиб и кручение мм2.
А – площадь поперечного сечения, мм2
Частные коэффициенты запаса прочности по нормальным Sтσ и касательным напряжениям Sт τ равны [3]:
Sт σ = σт /σ; Sт τ = τт /τ (5.10)
Общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений
Sт = 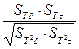 (5.11)
(5.11)
Статическую прочность считают обеспеченной, если Sт ≥[Sт], где [Sт] = 1,3…2,0 – минимально допустимые значения общего коэффициента запаса по текучести, которые назначают в зависимости от ответственности конструкции и последствий разрушения вала.
Момент сопротивления W при изгибе, Wk – при кручении и площадь А вычисляют по сечению:
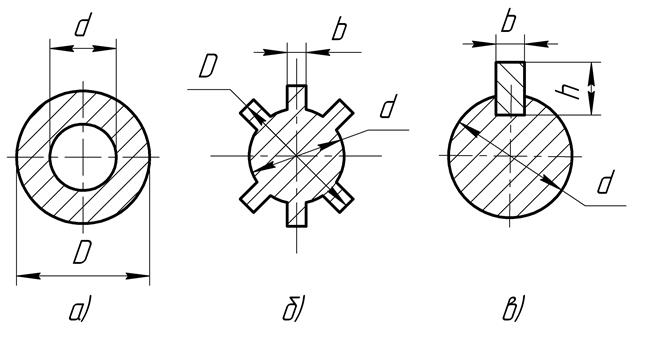
Рис. 5.5
Для сплошного круглого сечения диаметром D:
W =πD3 /32; Wк = πD3 /16; A = πD2 /4 (5.12)
Для полого круглого сечения (рис.5.5а)
W = ζw πD3 /32; Wк = ζw πD3 /16; A = π(D2 – d2) /4
где ζw = 1- (d ⁄ D)4 - коэффициент пересчёта.
Для вала с прямобочными шлицами (рис.5.5б):
W = [πd4 +в·z(D –d)(D + d)2] /(32D)
Wк =2W; А = πd2 /4 + в·z(D –d)/2
Для вала с одним шпоночным пазом (рис.5.5.в)
W = πd3/32 - в·h(2d –h)2 /16d; Wк = πd3/16 – в·h(2d – h)2/16d;
А = πd2/4 – в·h/2.
Расчёт на сопротивление усталости
Расчёты на сопротивление усталости предусматривают оценку влияния разновидности цикла напряжений, статических и динамических характеристик материалов, размеров, формы и состояния поверхностей деталей.
Расчёт выполняют в форме проверки коэффициента запаса прочности S, минимальное допустимое значение которого принимают в диапазоне [S] = 1,5 …2,5 в зависимости от ответственности конструкции и последствий разрушения вала, точности определения нагрузки и так далее.
Для каждого из опасных сечений вычисляют коэффициент S:
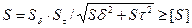 (5.13)
(5.13)
где Sσ и Sτ - коэффициенты запаса по нормальным и касательным напряжениям, определяемые по зависимостям:
Sσ = σ-1D/(σа +ψσD σm); Sτ = τ-1D/(τа +ψτD·τm) (5.14)
здесь σа и τа - амплитуды напряжений цикла;
σm и τm – средние напряжения цикла;
ψσD и ψτD – коэффициенты чувствительности к асимметрии цикла напряжений для рассматриваемого сечения. В расчётах валов принимают, что нормальные напряжения изменяются по симметричному циклу (σа = σп и σm = 0), а касательные напряжения по отнулевому циклу (τа = τк/2); τm = τk /2; тогда:
Sσ = σ-1D /σa (5.15)
Напряжения в опасных сечениях вычисляют по формулам:
σа = σп = 103·M/W; τа = τк/2 = 103Mk/2Wk (5.16)
где 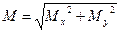 - результирующий изгибающий момент, Н·М
- результирующий изгибающий момент, Н·М
Мк – крутящий момент (Мк = Т); Н·М; W и Wк - моменты сопротивления сечения вала при изгибе и кручении, мм3.
Пределы выносливости вала в рассматриваемом сечении:
σ-1D =σ -1 / Kσ D; τ-1D = τ-1 /Kτ D (5.17)
где σ-1 и τ-1 - пределы выносливости гладких образцов при симметричном цикле изгиба и кручения (табл.5.1)
Кσ D и Kτ D – коэффициенты снижения предела выносливости.
Значения Кσ D и Kτ D вычисляют по зависимостям:
Kσ D =(Кσ ⁄ Кd σ +1 ⁄ КF σ – 1) ⁄ Кv (5.18)
Kτ D = (Кτ ⁄ Кd τ +1⁄ К F τ –1) ⁄ Кv
где Кσ и Кτ -эффективные коэффициенты концентрации напряжений, Кd σ и Кd τ - коэффициенты влияния абсолютных размеров поперечного сечения (табл.5.2); КF σ и К F τ - коэффициенты влияния качества поверхности; Кv - коэффициент влияния поверхностного упрочнения. Значения коэффициентов Кσ и Кτ берутся из таблиц 5.3; 5.4.
Таблица 5.2
| Напряжённое состояние и материал | Кd σ ( Кd τ ) при диаметре вала d, мм | |||||
| Изгиб для углеродистой стали | 0.92 | 0.88 | 0.85 | 0.81 | 0.76 | 0.71 |
| Кручение для всех сталей и изгиб легированной стали | 0.83 | 0.77 | 0.73 | 0.70 | 0.65 | 0.59 |
Таблица5.3
| Вид механической обработки | Параметр шерохова- тости Rа, мкм | КF σ при σв, МПа | К F τ при σв, МПа | ||
| ≤ 700 | >700 | ≤ 700 | >700 | ||
| Шлифование тонкое | до 0.2 | ||||
| Обтачивание тонкое | 0,2…0,8 | 0,99…0,93 | 0,99…0,91 | 0,99…0,96 | 0,99…0,95 |
| Шлифование чистовое | 0,8…1,6 | 0,93…0,89 | 0,91…0,86 | 0,96…0,94 | 0,95…0,92 |
| Обтачивание чистовое | 1,6…3,2 | 0,89…0,86 | 0,86…0,82 | 0,94…0,92 | 0,92…0,89 |
Таблица 5,4
| Вид упрочнения поверхности вала | Значение Кv при | ||
| Кσ =1,0 | Кσ =1,1…1,5 | Кσ ≥1,8 | |
| Закалка ТВЧ | 1,3 …1,6 | 1,6 …1,7 | 2,4 … 2,8 |
| Азотирование | 1,15…1,25 | 1,3… 1,9 | 2,0 …3,0 |
| Накатка роликом | 1,2 … 1,4 | 1,5 …1,7 | 1,8 … 2,2 |
| Дробеструйный наклёп | 1,1 … 1,3 | 1,4 … 1,5 | 1,6 … 2,5 |
| Без упрочнения | 1,0 | 1,0 | 1,0 |
Пример расчёта вала на прочность
Рассчитать тихоходный вал двухступенчатого цилиндрического редуктора при следующих исходных данных: силы в зацеплении
Ft = 4000 H; Fr =1485 H; Fа =813 Н; вращающий момент на валу
Т = 400 Н·М; делительный диаметр расположенного на валу зубчатого колеса d = 200 мм.
Необходимые для расчёта размеры вала принимаем из эскиза редуктора: l 1 =44мм; l 2 = 88мм; l 3 = 71мм;
1.Составляем расчётную схему вала
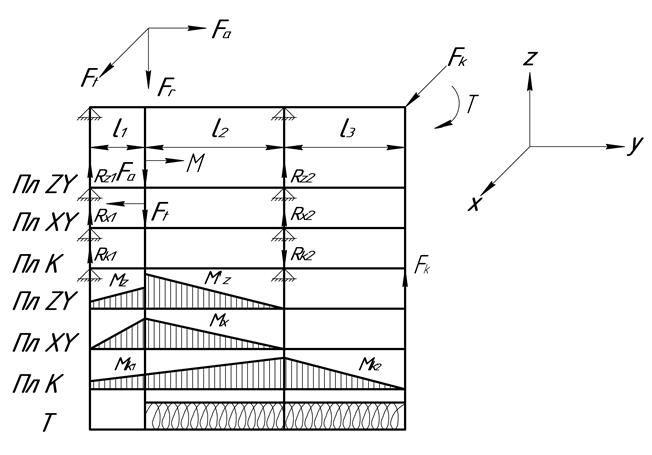
Рис. 5,6 Схемы нагружения вала
Определим дополнительные нагрузки, для чего векторы сил Ft; Fr и Fa прикладываем к точке, соответствующей центру крепления колеса на оси вала. В этом случае возникают пары сил, то есть возникают соответственно вращающий и изгибающий моменты:
T = Ft · d ⁄ 2 = 4000·0,2 ∕ 2 =400 Н.М.
М = Fa · d ⁄ 2 = 813·0,2 ⁄ 2 = 81,3 Н.М.
Консольная нагрузка Fк определяется по формуле для тихоходного вала
Fк = 250 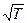
Fк = 250 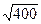 = 5000 Н.
= 5000 Н.
2 Для определения реакций опор используем уравнения статики:
В плоскости ZY должно выполняться условие:
∑МZ2 = 0; RZ!· (l1 + l2) + М – Fr · l2 = 0
откуда RZ! = 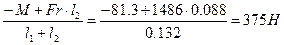
Исходя из условия ∑МZ1 = 0; т.е. RZ2· (l1 + l2) – М – Fr · l1 = 0
получаем RZ2 = 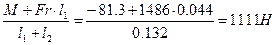 .
.
В плоскости XY в соответствии с условием: ∑МХ2 = 0:
RX1 ·(l1 + l2 ) –Ft·l2 =0
RX1 = 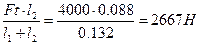 .
.
Из условия: ∑Fi =0; т.е. RX! – Ft + RX2 =0:
RX2 = Ft – RX! = 4000–2667 = 1333 Н.
Определяем реакции опор от консольной нагрузки Fк:
Из условия ∑МК2 = 0 или – RК1 ·(l1 + l2 ) –FК·l3 =0 имеем:
RК1 = 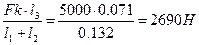
Поскольку RК1–R К2+ FК =0, то: R К2= RК1+ FК=5000+2690=7690 Н.
3. Определяем изгибающие моменты:
В плоскости ZY в сечении 1 -1:
MZ1 = RZ1 · l1= 375 · 0,044 =16,5H.M.
MZ1 = MZ1 + M = 16,5 + 81,3 = 97,8 Н.М.
В плоскости XY в сечении 1 – 1:
MХ1 = RХ1 · l1 = 2667 · 0,044 = 117,4 Н.М.
В плоскости консольной нагрузки:
В сечении 1-1: MК1 = RК1 · l1 = 2690 · 0,044 = 118,4 Н.М.
В сечении 2-2: MК2 = FК · l3 =5000 · 0,071 = 355 Н.М.
Строим эпюры изгибающих моментов MZ , MХ и MК
Суммарный изгибающий момент в сечении 1 – 1:
М∑1 = 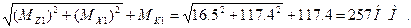
М́∑ = 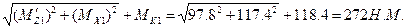
В сечении 2-2
М∑2 =МК2 =355 Н.М.
Сравнивая полученные значения суммарных изгибающих моментов, определим как наиболее опасное сечение 2-2, где расположена опора 2.
4. Выполняем эскиз вала (Рис.5.7)
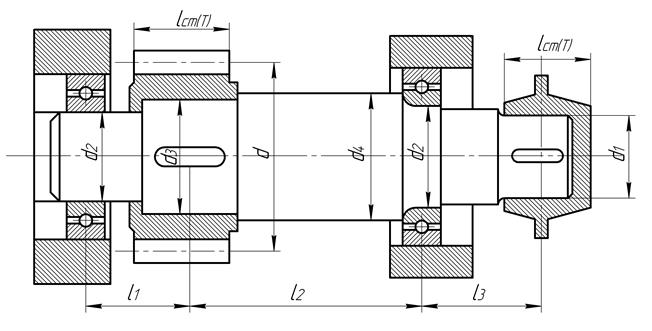
Рис.5.7 Эскиз вала.
Диаметры ступеней вала определим следующим образом.
Диаметр выходного участка вала вычисляем по формуле:
d = 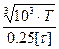 (5.19)
(5.19)
d1 = 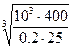 = 43мм
= 43мм
Принимаем d1 =42мм; диаметр вала под подшипник
d2 = d1 + (3…..7)мм; принимаем d2 = 45мм.
Диаметр вала под колесо d3 = d2 + (3 … 7)мм; принимаем
d3 =48мм. Диаметр буртика (уступа) d4 = d3 +(5 … 10)мм. Откуда
d4 =55мм
5. Проверочный расчёт вала на сопротивление усталости выполняем с определением коэффициента запаса усталостной прочности в сечении 2-2, используя формулу (5.13)
Коэффициент запаса прочности по напряжениям изгиба:
Sσ = 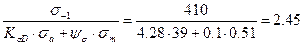
По напряжениям кручения:
Sτ= 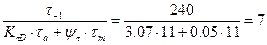
Вал изготовлен из стали 40Х с характеристиками:
НВ ≥ 270; σ -1 = 410МПа; τ -1 = 240МПа; ψσ = 0,1; ψτ = 0,05.
Переменные составляющие циклов изменения напряжений изгиба и кручения:
σа = 103 М∑ ⁄ W0 ; τа = τm = 0,5T ⁄ Wp ;
где W0 = 0,1d3 и Wp = 0,2 d3 - моменты сопротивления изгибу и кручению вала.
σа = 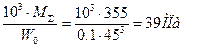
τа = 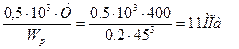
Постоянные составляющие циклов напряжений
σm =Fa ⁄ A = 813 · 4 ∕ (3,14·452 ) = 0,51 МПа.
τm = τa =11 МПа.
Общие коэффициенты концентрации напряжений
КσD = 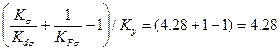
КτD = 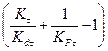 /Ку
/Ку 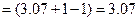
По таблицам 5.2 - 5.4 находим: Кσ ⁄ Кd σ = 4,28; Kτ ⁄ Kdτ = 3,07.
По таблице 5.3 коэффициент КF = 1 (поверхность шлифованная).
Коэффициент Кy =1.
Коэффициент запаса прочности в сечении 2-2:
S = 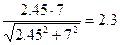
Значение коэффициента запаса прочности S превышает допустимое значение [S] равное 2, значит сопротивление усталости вала обеспечено.
5.3 Расчёт деталей БМП на вибрацию.
Рабочие органы и детали машин бытового назначения воспринимают внешние активные нагрузки: движущие моменты, полезные сопротивления, моменты трения и так далее. В большинстве случаев нагрузки не остаются постоянными во времени, а изменяются, как правило, по периодическим законам. Вследствие этого детали машин подвержены циклическому нагружению, и при наличии упругости в них возникают колебания. Так, в машинах бытового назначения возникают вибрации валов рабочих барабанов стиральных машин, машин химической чистки, деталей обувных машин, швейных машин, пылесосов и др. [1]
В результате действия вибрации снижаются точность обработки изделий, надёжность механизмов и систем автоматики, ускоряется износ деталей, ухудшаются условия труда вследствие появления шума и так далее. Поэтому очень важно прогнозирование вибраций и знание методов борьбы с ними.
Большинство машин бытового назначения характеризуется периодичностью нагружения и деформирования как отдельных звеньев, так и элементов конструкций, в частности, опор. Под действием периодически изменяющейся возмущающей силы по гармоническому закону P =P0 sinωτ возникают вынужденные колебания, которые могут быть гармоническими и случайными (Рис.5,8).
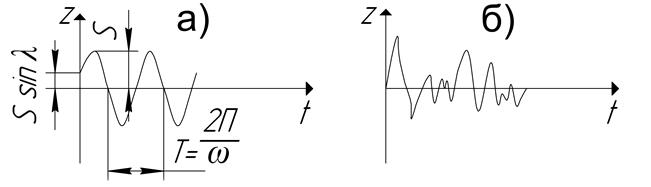
Рис 5.8 Виды колебаний
а – гармонические; б – случайные
Для гармонической вибрации справедливо следующее выражение:
Х(t) = А · sinωt (5.20)
где Х(t) – смещение от положения равновесия в момент времени t ; А- амплитуда перемещения; ω=2πf – угловая частота 1⁄ с .
Виброскорость и виброускорение элемента конструкции находят посредством дифференцирования выражения для виброперемещения:
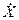 (t) = ω·А· cosωt (5.21)
(t) = ω·А· cosωt (5.21)
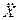 (t) = -ω2·A·sinωt (5.22)
(t) = -ω2·A·sinωt (5.22)
Для описания гармонической вибрации часто используется комплексная форма записи вида:
Х(t) = А ·eiωt
Таким образом, основными характеристиками гармонической вибрации являются амплитуды виброперемещения, виброскорости, виброускорения и угловая частота колебаний.
Гармоническая вибрация часто характеризуется коэффициентом виброперегрузки nв:
nв = 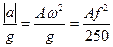 (5.23)
(5.23)
где А – амплитуда колебаний, мм; f – частота, Гц;
а- амплитуда виброускорения.
Вибрация, параметры которой (амплитуда, частота и др.) изменяются во времени случайным образом, называется случайной (рис.5.8 б). Она может быть стационарной и нестационарной. У стационарной вибрации математическое ожидание виброперемещения равно нулю, матожидание виброскорости и виброускорения постоянны; у нестационарной же вибрации постоянства статистических характеристик не наблюдается. Такого рода вибрации возникают, например, при движении транспортных средств.
Практически любое тело (деталь) имеет собственную частоту колебаний. При совпадении частоты возмущающей силы с частотой собственных колебаний системы наступает её критическое состояние, называемое резонансом. Оно связанно с потерей устойчивости, что приводит к большим деформациям, часто превосходящим допустимые значения. Наиболее подверженными вибрации являются детали типа стержней с различно-закреплёнными концами. Чаще всего в конструкциях машин и агрегатов БМП встречаются детали типа двухопорных стержней с распределённой или сосредоточенной нагрузкой (рис.5.9)
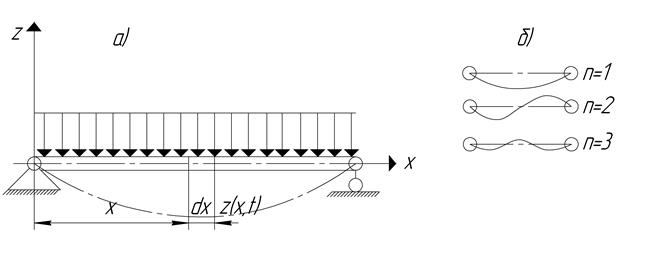
Рис 5.9. Изгибные колебания стержня
а – схема нагружения; б – формы колебаний.
Частота собственных колебаний таких стержней определяется посредством уравнения типа
ω0i = 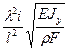 (5.24)
(5.24)
где λi – корень уравнения частот изгибных колебаний;
l – длина стержня; Е – модуль упругости материала стержня;
Jy- момент инерции сечения стержня; ρ – плотность материала;
F – площадь сечения стержня.
Корни частотного уравнения sin λ = 0 составляют :
λ =i·π; (i = 1,2, …..n).
Так, для стержня прямоугольного сечения, у которого F = b· h,
Jy = b h3 ⁄ 12;
ω0i = 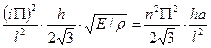 (5.25)
(5.25)
Таким образом, собственная частота стержня прямоугольного сечения зависит от его длины и толщины и не зависит от его ширины.
Для стержней, оба конца которых жёстко заделаны, величины λ имеют следующие значения:
λ1 =4,730; λ2 =7,853; λi = (2i +1)·π ∕2, (i≥3).
Подставляя значение λi в уравнения (5.24 и 5.25), получим собственные частоты стержня ω0i.
Анализ уравнения (5.24) показывает, что стержень имеет бесконечное число собственных колебаний (частот), при этом частоты всех тонов быстро возрастают. Из (5.24) также видно, что любая собственная частота стержня сильно зависит от его длины (обратно пропорционально квадрату длины) и в меньшей степени зависит от размеров и формы поперечного сечения и свойств материала.
Это даёт возможность конструктору изменять частотные характеристики разрабатываемой конструкции в нужную сторону.
5.4 Расчёт деталей БМП при ударных нагрузках.
Ударные нагрузки возникают при резком изменении скоростей движения деталей в момент их соприкосновения. При ударе возникают нагрузки, которые в несколько раз превышают статические, что может привести к большим деформациям и разрушению деталей.
Важным фактором, определяющим характер нагружения системы, является время нарастания нагрузки от нуля до первого максимума с учётом собственных колебаний.
Для оценки влияния этого фактора на динамическую систему рассматривают соотношение времени нагружения τН и периода собственных колебаний системы Т.
Когда время нарастания нагрузки больше периода Т собственных колебаний, то есть τН ⁄ Т >5 … 10, то практически можно рассматривать такое воздействие как статическое. Если соотношение τН ⁄ Т <5, то нагружение считают динамическим. Для этого случая применяют методику расчёта для чисто ударного нагружения. Для условия 0,5< τН ⁄ Т <5 применяют методику расчёта квазиударного нагружения.
Квазиударное нагружение характерно для момента пуска отдельных механизмов; ударов, вызванных разрывом кинематической цепи из-за наличия зазоров в местах соединения звеньев; амортизации и демпфирования удара больших масс при их остановке и т.д.
Конечным результатом расчётов при ударном и квазиударном нагружениях обычно является определение максимальных усилий и напряжений в звеньях системы; определение допустимых зазоров, исключающих разрывы кинематических цепей, и, в некоторых случаях. определение закона движения звеньев.
Поскольку точный расчёт деталей на ударную нагрузку является весьма сложным, практически расчёт на прочность при ударе производят по формулам, принятым для статического нагружения.
Условие прочности принимается в виде:
σmax = kД σ cmmax ≤ [ σдоп ] (5.26)
где kД–коэффициент динамичности; kД= fД ∕ fст; [ σдоп ] - допустимое напряжение; коэффициент динамичности kД в простейших случаях определяют расчётным путём, а в сложных опытным путём.
Если нагрузка прикладывается мгновенно, то kД =2; если нагрузка мгновенно меняет знак, то kД =3.
При ударе груза со скоростью V посредине балки, лежащей на двух опорах, коэффициент динамичности
KД = 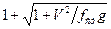 (5.27)
(5.27)
При продольном ударе груза по балке длиной l
KД = 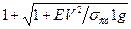 ( 5.28)
( 5.28)
где fcт - статический прогиб балки; E – модуль упругости;
σcт – напряжение при статической нагрузке.
При ударе без учёта массы ударного тела то, когда m0 <<m,
KД = 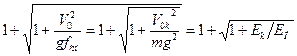 (5.29)
(5.29)
где m –масса ударяющего тела;
Ек = 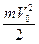 -кинетическая энергия движения массы m к моменту соударения;
-кинетическая энергия движения массы m к моменту соударения;
En = mgfcт ⁄ 2 потенциальная энергия упругой деформации ударяемого тела при статическом действии массы m;
k - жёсткость ударяемого тела при данном виде деформации.
Если масса ударяемого тела очень велика, то коэффициент динамичности принимается равным 2.
При уменьшении ударных нагрузок, испытываемых механизмом, необходимо предусмотреть рациональное построение механизма, выбор оптимальных законов движения, уменьшение массы движущихся частей; подбор соотношения периодов собственных колебаний, механизма и нагрузок, применение демпфирования, уравновешение и так далее.
5.5 Способы борьбы с вибрацией и ударом
Выбор того или иного способа защиты от механических воздействий зависит от вида воздействия и характера возмущающих сил, от частотного диапазона возмущений и от конструктивных особенностей механизма. Применение виброизоляции (амортизаторов) позволяет ослабить влияние вибрации и ударов на надёжность и устойчивость функционирования аппаратуры [4]. Исследования показывают, что на высоких частотах (υ> 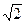 ) (υ = ω ∕ ω0 –частотное отношение) достигается уменьшение амплитуды вибросмещения и виброускорения исследуемой конструкции.
) (υ = ω ∕ ω0 –частотное отношение) достигается уменьшение амплитуды вибросмещения и виброускорения исследуемой конструкции.
Таким образом, если нижняя граница диапазона возмущающих частот соответствует значениям υ≥ 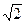 , применение амортизаторов целесообразно.
, применение амортизаторов целесообразно.
Когда нижняя граница возмущающих частот соответствует значениям υ< 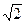 вывод о целесообразности применения амортизаторов зависит от характера возмущающих сил. Если эти силы носят случайный характер, то о степени опасности низкочастотных возмущений можно судить на основании спектрального анализа.
вывод о целесообразности применения амортизаторов зависит от характера возмущающих сил. Если эти силы носят случайный характер, то о степени опасности низкочастотных возмущений можно судить на основании спектрального анализа.
Если спектральная функция возмущающих сил имеет максимум в области низких частот, то при эксплуатации будут превалировать низкочастотные воздействия. Они могут вызвать интенсивные резонансные колебания аппаратуры и удары подвижных частей амортизаторов об ограничители хода. В таких случаях целесообразно отказаться от амортизаторов и применять другие способы защиты. В целом же, для защиты аппаратов от удара желательно применение амортизаторов. Наилучшие результаты могут быть получены при использовании амортизаторов с нелинейной характеристикой. В настоящее время существует множество различных типов амортизаторов, отличающихся как по виду упругого элемента, так и по конструктивному исполнению. Конструктор изделий сталкивается с задачей выбора амортизаторов, наилучшим образом удовлетворяющих техническим требованиям задания в условиях конкретной эксплуатационной обстановки.
Наряду с применением амортизаторов находит применение другой способ виброизоляции, заключающийся в том, что на пути распространения упругих волн ставятся экраны в виде воздушных зазоров, а также прокладок из материалов, отличающимся по своим упругим характеристикам от материалов конструкций и так далее. Однако этот способ эффективен только на высоких частотах.Наибольшее применение в области вибро-ударозащиты получили способы, направленные на уменьшение или устранение резонансных колебаний. Так, при низкочастотных внешних воздействиях часто применяют смещение спектра собственных частот колебаний конструкции за верхнюю границу частот возмущающих вибраций. Для полного устранения резонансных колебаний необходимо, чтобы первая собственная частота колебаний f0 была не менее чем на октаву выше максимальной частоты возмущающих колебаний fв [4], то есть необходимо выполнение условия: f01 ∕ fв ≥2.
Практически это может быть достигнуто изменением способов крепления конструкции и постановкой дополнительных опор.
Одним из путей решения проблемы снижения резонансных колебаний является улучшение демпфирующих свойств конструкций, то есть повышение рассеяния энергии колебаний за счёт сил трения. Это достигается включением в конструкции деталей специальных демпфирующих покрытий из вибропоглощающих материалов, внутреннее трение которых в десятки и сотни раз больше, чем у конструкционных материалов. Преимущество этого способа состоит в том, что резонансные колебания могут быть снижены в широком диапазоне частот при незначительном увеличении массы и габаритов конструкции. Использование рассмотренных способов уменьшения резонансных колебаний требует от конструктора умения рассчитывать собственные частоты колебаний, амплитуды перемещений и виброускорений а также принятия необходимых мер, обеспечивающих качественную конструкцию.
6. Расчёт резьбовых, сварных и заклёпочных соединений.
В машиностроении в частности, в производстве БМП, применяют следующие соединения деталей и узлов: разъёмные: резьбовые, шпоночные, зубчатые, штифтовые, клиновые; и неразъёмные: сварные, заклёпочные, паяные, клеевые и прессовые. Наиболее распространёнными видами соединений, широко применяемыми в БМП, являются резьбовые и сварные соединения.
6.1 Расчёт резьбовых соединений.
Широкое применение резьбовых соединений объясняется их достоинствами: высокой нагрузочной способностью и надёжностью; удобством в эксплуатации; относительной простотой конструкции; малыми размерами и массой, невысокой стоимостью и весьма высокой степенью стандартизации [2].
Основным недостатком резьбовых соединений является высокая концентрация напряжений в резьбе, снижающая их прочность, особенно при циклических нагрузках. Причиной выхода из строя резьбовых соединений являются чаще всего разрушения стержня болта (винта, шпильки) или резьбы.
Стандартные резьбовые соединения рассчитывают по наименее прочному элементу – стержню болта (винта, шпильки). По найденному диаметру болта подбирают другие элементы резьбового соединения: гайки, шайбы и др.
Длина болта принимается в зависимости от толщины соединяемых деталей. Расчёт болтов зависит от характера нагружения и особенностей сборки резьбовых соединений (затянутые, незатянутые, с зазором и без зазора).По характеру нагружения соединения подразделяют на статически или циклически нагружённые, воспринимающие осевую или поперечную (сдвигающую) нагрузку.
6.1.1. Расчёт статистически нагруженных болтов. При осевом нагружении условие прочности на растяжение имеет вид:
σ = 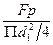 (6.1)
(6.1)
Тогда расчётный внутренний диаметр по резьбе
d1 ≥ 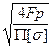 (6.2)
(6.2)
где Fр - расчётное усилие в болте; [σ] – допустимое напряжение растяжения для материала болта.
[σ] = 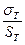 (6.3)
(6.3)
где σт – предел текучести материала болта;
Sт - коэффициент запаса прочности, зависящий от материала, характера нагрузки и диаметра резьбы d, которым прирасчёте задаются (таблица 6.1)
Таблица 6.1
Коэффициент запаса прочности Sт
| Нагрузка | Диаметр Резьбы, мм | Сталь | |
| Углеродистая | Легированная | ||
| Постоянная | М6 … М16 М16…М30 | 5 … 4 4 … 2,5 | 6,5 … 5 5 … 3,3 |
| Переменная (от 0 до F) | М6 … М16 М16…М30 | 10 …6,5 6,5 | 12,5…8,3 8,3 |
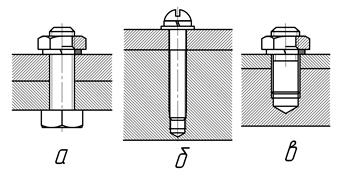
Рис. 6.1
Резьбовые соединения
а - болтовое; б – винтом; в – шпилькой
Если в результате расчёта получается значение d , не удовлетворяющее разработчика, задаются другие значения диаметра и расчёт повторяют.
При контролируемой затяжке болтов из углеродистых сталей принимают: [σ] ≈ 0,6σт; легированных [σ] ≈ 0,5σт. Для незатянутых резьбовых соединений из сталей: углеродистых [σ] = (0,5… 0,6)σт ; легированных [σ] = (0,4… 055)σт.
Расчётное усилие Fр в формулах (6.1; 6.2) определяют в зависимости от вида осевого нагружения. Рассмотрим несколько типичных случаев нагружения.
1. Болт затянут и к нему приложена внешняя осевая нагрузка.
В этом случае расчетные усилия в болте
Fр = 1,3 F + χ ·Fвн (6.4)
где 1,3 – коэффициент, учитывающий напряжение в болте вследствие его скручивания при затяжке;
F – усилие начальной затяжки, соответствующее моменту завинчивания Тзв , создаваемому ключом; (Тзв ≈ 0.2 F· d);
χ - коэффициент внешней нагрузки, зависящий от коэффициентов податливости болта λБ и соединяемых деталей λД
χ = 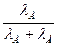 (6.5)
(6.5)
В приближённых расчётах для соединений из стали и чугуна без упругих прокладок принимают χ = 0,2 … 0,3; при наличии упругих прокладок χ = 0,4 … 0,5.
Во избежание раскрытия стыка принимают:
F = Кзт(1─ χ ) Fвн (6,6)
где Кзт - коэффициент начальной затяжки, принимаемой при постоянной нагрузке Кзт = 1,25 … 2; при переменной нагрузке и для обеспечения герметичности Кзт = 2,5 … 4.
Выразив силу начальной затяжки F через внешнюю нагрузку Fвн (зависимость 6.6) и подставив её в выражение (6.4), получим расчётное усилие в болте:
FP = 1,3 Кзm (1─ χ )Fвн + χ ·Fвн (6.7)
Другие виды осевого нагружения болтов являются частными случаями рассмотренной задачи.
2. Болт затянут, внешняя нагрузка отсутствует.
Так как Fвн равно нулю, то расчётное усилие в болте равно:
Fр = 1,3 F (6.8)
Вычисленное значение внутреннего диаметра d1 позволяет по данным [2. таб. 16.3] определить наружный диаметр d и шаг резьбы Р.
6.1.2. Расчёт резьбовых соединений при переменных нагрузках
Причиной потери работоспособности таких резьбовых соединений является усталостное разрушение стержней болтов (винтов, шпилек) в месте перехода резьбовой части в гладкую.
Болт, диаметр которого определен по формуле (6.2), проверяют на усталостную прочность с использованием коэффициента запаса по амплитуде цикла:
Sа = 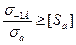 (6.9)
(6.9)
где σ-1- предел выносливости болта;
σ-1б = 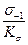
 (6.10)
(6.10)
здесь σ-1 - предел выносливости при растяжении гладкого образца (см. табл.6.2);
Кσ - эффективный коэффициент концентрации напряжения, принимаемый при затянутом резьбовом соединении для углеродистой стали Кσ =3,5 … 4,5; для легированной стали
Кσ = 4,0 … 5,5;
σа - амплитуда цикла:
σа = 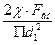 (6.11)
(6.11)
Допустимый коэффициент по амплитуде цикла [Sа] =2,5.
В резьбовых соединениях, подверженных переменным нагрузкам, ослабление затяжки происходит значительно интенсивнее, чем при постоянных нагрузках. Это отрицательно влияет на усталостную прочность, т.к. приводит к увеличению амплитуды переменной внешней нагрузки, а также является причиной самоотвинчивания резьбовых соединений.
Чтобы предотвратить самоотвинчивание, стопорят гайки и болты относительно друг друга или корпусных деталей.
Таблица 6.2
| Марка стали | Предел прочности σв МПа | Предел текучести σт МПа | Предел выносливости σ -1 МПа |
| Ст3 … Ст10 | |||
| 30х | |||
| 30хГСА | |||
| ВТ 16 | - |
Существуют различные способы стопорения, основными из которых являются применение контргаек, пружинных шайб (шайб Гровера), шплинтов.
В целях повышения надёжности резьбовых соединений, подверженных переменным нагрузкам, целесообразно применять начальную затяжку соединений, равную (0,6 … 0,7) σт для болтов из углеродистых сталей и (0,5 … 0,6) σт для легированных сталей.
6.1.3. Расчёт резьбовых соединений, воспринимающих поперечную нагрузку.
Условием надёжности таких соединений является отсутствие сдвига деталей в стыке. Здесь возможны два варианта конструкций.
1. Болт установлен с зазором
Во избежание сдвига деталей резьбового соединения необходимо затянуть его так, чтобы сила трения FТ на стыке деталей была больше сдвигающей силы Q:
FТ=f · F · Z · i ≥ Q (6.12)
где f – коэффициент трения (f =0,15 … 0,2);
F – необходимая сила затяжки;
Z- число болтов;
i - число стыков.
Тогда необходимая сила затяжки F:
F = 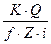 (6.13)
(6.13)
где к – коэффициент запаса; к = 1,2 … 1,5 при статической нагрузке;
к = 1,8 … 2,0 – при переменной нагрузке.
2. Болт вставлен в отверстие без зазора.
В этом случае диаметр стержня болта d0 выполняют с допуском, обеспечивающим посадку без зазора.
Затяжка болта необязательна, а поэтому силы трения в стыке не учитываются. Поперечная сдвигающая сила Q действует непосредственно на болт, который испытывает напряжение среза:
τср = 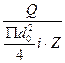 ≤ [τср]] (6.14)
≤ [τср]] (6.14)
Откуда диаметр стержня болта
d0 = 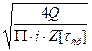 (6.15)
(6.15)
где i –число поверхностей среза;
Z – число болтов;
[τср] = (0,2 …0,3)σт .
При постановке болтов без зазора болты получаются значительно меньшего диаметра, чем при постановке с зазором и работающие «на затяжку». Однако, технологически конструкции с болтами, поставленными без зазора, значительно сложнее, что ограничивает их применение.
6.1.4. Примеры расчёта резьбовых соединений.
Пример 1.
Определить необходимый диаметр болтов из стали Cт3 крепления крышки радиально-упорного подшипника, если осевая сила, воспринимаемая подшипником, Fа = 3300Н; число болтов Z=6; коэффициент запаса затяжки Кзт = 3; коэффициент внешней нагрузки χ =0,3.
1. Определим внешнюю нагрузку, приходящуюся на один болт:
Fвн = 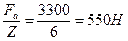
2.По формуле (6.7)находим расчётную нагрузку, воспринимаемую одним болтом.
Fр = 1,3 Кзт(1-χ)Fвн +χFвн = 1,3 ·3(1─0,3)·550 + 0,3·550 = 1667Н.
3.Вычисляем расчётный внутренний диаметр резьбы болта
d1 = 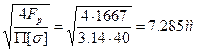
Здесь [σ] = 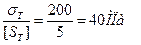 . Значение [Sт] принимаем из
. Значение [Sт] принимаем из
таблицы 6.1. Выбираем болт М10 (d1 = 8,376мм).
Пример 2.
Рассчитать болты крепления кронштейна, если действующая на них нагрузка Q1 равна 1100Н.; материал болта Ст3 (σт =200МПа).
1-й случай – болты установлены с зазором.
1. Приняв коэффициенты трения в стыке f = 0,15 и запаса к=1,3, определим по формуле (6.13) необходимую силу затяжки болтов:
F = 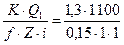 = 9533Н.
= 9533Н.
2. По таблице 6.1 в зависимости от предполагаемого диаметра принимаем Sт = 4 и тогда:
[σ] = 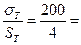 50 МПа.
50 МПа.
3. В соответствии с (6.2) и (6.8) находим:
d1 = 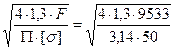 =17,8мм.
=17,8мм.
С учётом полученного диаметра d1 корректируем значение Sт = 3,5, и тогда значение [σ] = 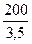 =57МПа;
=57МПа;
а d1 = 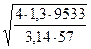 = 16,64мм.
= 16,64мм.
Этому значению d1 соответствует болт М18 (d1 =14,9мм при р = 2,5).
2-й случай – болты установлены без зазора.
Определим диаметры болтов, установленных без зазора (под развёртку) из условия прочности на срез по формуле (6.15):
d0 = 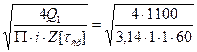 =4,83мм.
=4,83мм.
где [τер] = 0,3σТ =0,3·200 = 60МПа.
Расчёт показывает, что в этом случае могут быть применены болты диаметром гладкой поверхности стержня d0 = 5мм и резьбы М4. Однако, по технологическим соображениям этот вариант установки болтов нерационален.
6.2 Расчёт сварных соединений.
Сварные соединения – это наиболее распространённые неразъёмные соединения, применяемые в машиностроении и приборостроении.
Они обладают рядом преимуществ:
- проще обеспечивают условия равнопрочности детали;
- снижают стоимость изделия благодаря относительно малой трудоёмкости процесса сварки;
- снижают массу конструкции (примерно на 20 – 25% меньше клёпаной);
- обеспечивают герметичность и плотность соединений;
- позволяют автоматизировать процесс.
В ряде случаев сварку можно использовать не только для соединения деталей, но и как способ изготовления самих деталей (замена литья и ковки).
В то же время сварные соединения имеют ряд недостатков:
- они чувствительны к ударам и вибрациям;
- подвержены короблению из-за нагревания;
- чувствительны к виду свариваемых металлов.
Из различных способов сварки наиболее широкое применение нашла электродуговая сварка. Она осуществляется посредством местного нагрева деталей в зоне их соединения до расплавления, при котором возникают межатомные связи между свариваемыми элементами.
Различают три вида дуговой сварки: автоматическую, полуавтоматическую и ручную.
Автоматическая сварка под флюсом или в среде защитных газов позволяет сваривать самые разнообразные материалы, включая высокопрочные нержавеющие и жаропрочные стали, алюминиевые сплавы толщиной от долей мм. до десятков миллиметров. Она обеспечивает высокое качество шва, является высокопроизводительной и экономичной.
Полуавтоматическая сварка применяется для получения длинных швов в местах, недоступных для автоматической сварки, а также для коротких и прерывистых швов.
Ручная сварка применяется в тех случаях, когда другие способы сварки неприемлемы (трудный доступ шва и т.д.). Она мало производительна и качество её зависит от квалификации сварщика.
6.2.1.Конструкция сварных соединений и расчёт их на прочность.
Рассмотрим основные виды сварных соединений, выполненных электродуговой сваркой. Стыковые соединения (рис 6,2)
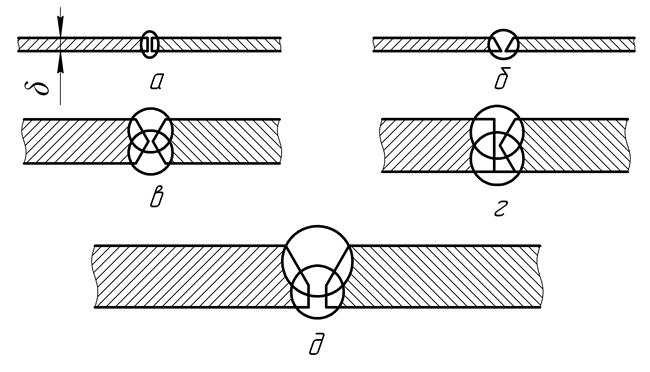
Рис.6.2 Стыковые соединения при различной толщине материала и форме кромок : а – δ ≤8мм; б- δ ≤ 16мм; в – δ= 12 – 40мм;
г - δ≤30мм; д - δ≤40мм.
Стыковые соединения наиболее просты и надёжны. Они имеют прочность, близкую к прочности основного металла, обеспечивают наименьшую массу и концентрацию напряжений. В зависимости от толщины δ деталей, сварку выполняют однострочным (рис 6.2, а,б) или двухстрочным (рис.6.2., в,г,д) швами. При средних и больших толщинах в целях улучшения качества специально обрабатывают кромки, выполняя прямолинейные или криволинейные скосы.
Встык сваривают также трубы, швеллеры, уголки и другие фасонные профили.
При воздействии внешней нагрузки сварные соединения разрушаются преимущественно в прилегающих к шву участках, поэтому расчёт стыкового соединения выполняют по размерам сечений в этой зоне.
Расчёты стыкового шва для разных видов нагрузки выполняют:
на растяжение: 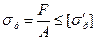 (6.16)
(6.16)
на сжатие: 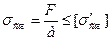 (6.17)
(6.17)
на изгиб: 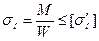 (6.18)
(6.18)
на изгиб с растяжением: 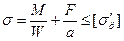 (6.19)
(6.19)
где F – растягивающая или сжимающая сила, Н; А – площадь расчётного сечения, мм2 ; М – изгибающий момент, Нмм; W – момент сопротивления расчётного сечения шва, мм3; [σ р] и
[σ сж] – допустимые напряжения растяжения и сжатия, МПа.
Нахлёсточные соединения (рис.6.3)
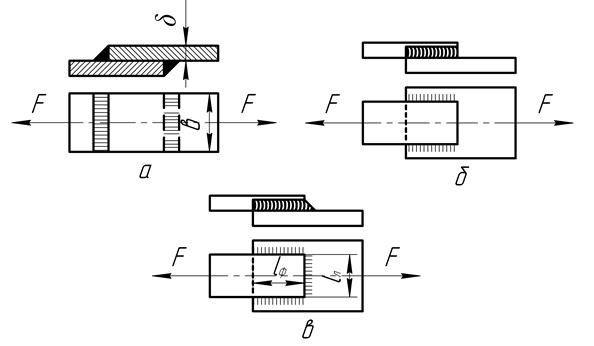
Рис.6.3.
Нахлёсточные соединения со швом:
а – лобовым; б – фланговым; в – комбинированным
Нахлёсточные соединения выполняют с угловыми (валиковыми) швами, причём разделки кромок не требуется. В зависимости от расположения швов по отношению к действующему на соединение усилию, различают лобовые (рис.6.3. а), фланговые (рис. 6.3. б) и комбинированные
(рис. 6.3. в) швы.
По форме поперечного сечения швы бывают нормальными, выпуклыми и вогнутыми и в виде неравнобедренного прямоугольного треугольника. (Рис 6.4. а,б,в,г)

Рис.6,4. Формы сечений угловых швов.
В основном применяют швы нормального сечения. Катет шва К обычно равен толщине листа δ. В машиностроении обычно принимают 3≤К≤20мм.
Все угловые швы рассчитывают на срез. Наиболее часто разрушение
 шва происходит по плоскостибиссектрисы ав прямого угла (рис.6.5). Высота шва h = К·cos450≈0,7К, а площадь среза Аср = 0,7 к·l, где l- длина шва. При симметричном расположении угловых швов относительно линии действия
шва происходит по плоскостибиссектрисы ав прямого угла (рис.6.5). Высота шва h = К·cos450≈0,7К, а площадь среза Аср = 0,7 к·l, где l- длина шва. При симметричном расположении угловых швов относительно линии действия
Рис. 6.5 растягивающей или сжимающей нагрузки
Расчетная схема (рис.6.3)принимают, что по всей длине периметра
углового шва. шва напряжение распределяется равномерно и
условие прочности имеет вид:
τ = 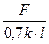 ≤[ τср ] (6.20)
≤[ τср ] (6.20)
где [ τср ] - допустимое напряжение на срез.
Поскольку в действительности по длине фланговых швов напряжение распределяется неравномерно, длину шва ограничивают lф ≤ 50К.
Напряжения в соединениях, нагруженных моментом М, распределяются по длине шва неравномерно. Расчёт таких соединений зависит от соотношения длины швов l и расстояния между ними в. (Рис.6.6)
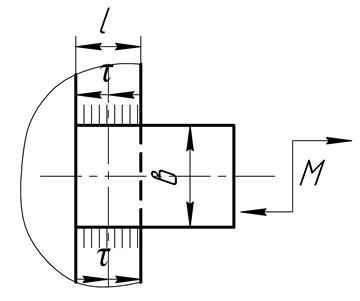
Рис. 6.6
Схема углового шва, нагруженного моментом.
При l ≥ b напряжение τ:
τ= М ⁄ Wр (6.21)
гдеWр – полярный момент сопротивления.
Для сравнительно коротких швов l<b на практике применяют приближённый расчёт по формуле:
τ = М ⁄ 0,7 к·l·в ≤[τср ] (6.22)
Тавровые соединения
Тавровые соединения применяют, когда элементы его расположены взаимно перпендикулярно. Такие соединения могут быть выполнены как без разделки кромок (рис.6.7 а), так и с односторонней или двухсторонней ( рис.6.7. б, в) разделкой.
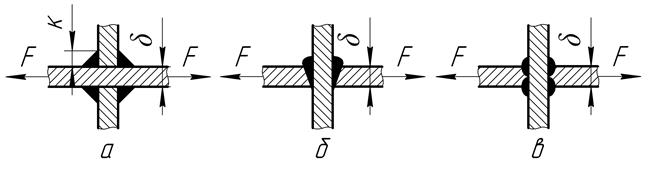
Рис.6.7 Тавровые соединения
При выполнении соединения угловым швом без разделки кромок (рис.6.7. а), его рассчитывают на срез:
τ = 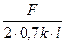 ≤[ τср ] (6.23)
≤[ τср ] (6.23)
где l – длина каждого из угловых швов.
Тавровые соединения с разделкой кромок рассчитывают как стыковые в зависимости от действующей нагрузки по формулам (6.16 … 6.19)
Допустимые напряжения для сварных соединений зависят от ряда факторов: способности материала к свариванию, вида технологического процесса и вида электродов, характера действующих нагрузок. [2]. Допустимые напряжения в сварных швах из низко- и среднеуглеродистых сталей при статической нагрузке приведены в таблице 6.3.
Таблица 6.3
| Сварка | Допустимые напряжения при: | ||
| Растяжении [σ р] | Сжатии [σ сж] | Срезе [τср ] | |
| Автоматическая под флюсом, ручная электродами Э42А и Э50А | [σ р] | [σ р] | 0,65[σ р] |
| Ручная электродами Э42 и Э50 | 0,9[σ р] | [σ р] | 0,6[σ р] |
Примечание: [σ р] = σ р ⁄ Sт – допустимое напряжение растяжения материала соединяемых деталей;
Sт - коэффициент запаса прочности.
Допустимые напряжения при переменных нагрузках определяют умножением табличных значений на коэффициент γ. Для углеродистых сталей его вычисляют по формуле:
γ = 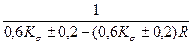 ≤1 (6.24)
≤1 (6.24)
где Кσ – эффективный коэффициент концентрации напряжений;
в знаменателе верхние знаки следует применять при напряжениях растяжения и при касательных напряжениях, а нижние – при напряжении сжатия; R – характеристика цикла напряжений:
R = 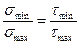 (6.25)
(6.25)
Таблица 6.4
Эффективный коэффициент концентрации напряжений Кσ
| Расчётный элемент | Низкоуглеродистая сталь Ст3 | Низколегированная сталь 15 СНА |
| Деталь в месте перехода к шву: стыковому лобовому фланговому | 1,5 2,7 3,5 | 1,9 3,3 4,6 |
| Угловые швы: лобовые фланговые | 2,0 3,5 | 2,0 4,5 |
Повышению выносливости сварн
Дата добавления: 2015-09-25; просмотров: 1695;
