Основные критерии работоспособности машин.

К основным критериям работоспособности машин и оборудования, применяемого в различных отраслях хозяйства, относятся прочность, жёсткость, износостойкость и, для некоторых деталей машин –теплостойкость и виброустойчивость.

Прочность - способность детали противостоять разрушению или возникновению пластической деформации в течение требуемого срока службы [2, 3].

При оценке прочности конструкции сравнивают рабочие напряжения, возникающие в деталях машин под действием нагрузок, с допустимыми напряжениями по условию

σ≤[σ] или τ≤[τ] (4.4)

где σ и τ - расчётные нормальные и касательные напряжения в опасном сечении детали; [σ] и [τ] - допустимые напряжения.

При одновременном действии напряжений изгиба (растяжения) σ и кручения τ расчёт ведут по эквивалентному напряжению:

σ_Е ≤ [σ] (4.5)

где σ_Е = 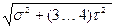- эквивалентное напряжение.

У деталей, работающих в контакте, под действием нагрузок в зоне контакта возникают местные напряжения и деформации. Под действием контактных напряжений происходит разрушение деталей.

Поэтому расчёт прочности в этом случае ведут по условию контактной прочности (формула Герца).

σ ≤ [σ_Н] (4.6)

σ_Н > 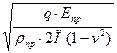(4.7)

где [σ] - допустимое контактное напряжение; q - нагрузка на единицу длины контакта; ς_пр - приведенный радиус кривизны контактируемых поверхностей; Е_пр - приведенный модуль упругости материалов контактных деталей; ν - коэффициент Пуассона.

Следует иметь в виду, что метод оценки прочности по допустимым напряжениям в опасной точке не даёт представлений о надёжности деталей, не раскрывает характер предполагаемого разрушения, режима нагружения и других

факторов, влияющих на надёжность. Также использование

допустимых напряжений затрудняется при действии переменных нагрузок.

Расчёт по допустимым напряжениям широко используется при проектировании для предварительной оценки размеров опасных сечений.

Более точный расчёт, применяемый для деталей машин – это расчёт по коэффициенту запаса прочности. Такой расчёт позволяет учесть ряд факторов, влияющих на прочность, а именно, концентрацию напряжений, размеры деталей и так далее.

При таком расчёте вместо условия прочности (4.4) , используют тождественные условия:

S = 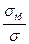≥[S]; S = 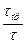≥[S]; (4.8)

где S – расчётный коэффициент запаса прочности; σ и τ - расчётное нормальное и касательное напряжения в опасной точке детали; [S] – допустимый коэффициент запаса прочности.

При действии статических нагрузок коэффициент запаса прочности Sσ принимается равным Sσ = σв ∕ σmax = 1,5… 2,0.

В случае действия переменных напряжений на прочность влияют такие факторы, как концентрация напряжений, асимметрия цикла, масштабный эффект и другие факторы.

При расчёте в этом случае определяют максимальные напряжения σmax и τmax

σ_max = σ_a ·К_σd + σ_m· Ψ_σ (4.9)

τ _max = τ_a · К_{τ d} + τ_m · Ψ_τ

где σ_a, σ_m,τ_a,τ_m - амплитудные и средние соответственно нормальные и касательные напряжения цикла;

К_σq =K_σ ⁄ K_σd + 1 ⁄ β-1; К_τq =K_τ ∕ K_τd + 1 ∕ β-1 – приведённые

эффективные коэффициенты концентрации соответственно нормальных и касательных напряжений в детали;

К σ и Кτ - эффективные коэффициенты концентрации нормальных и касательных напряжений;

Кσd - коэффициент, учитывающий диаметр заготовки детали;

β - коэффициент, учитывающий состояние поверхности (технологию изготовления);

Ψσ и Ψτ - коэффициенты, характеризующие влияние асимметрии цикла.

При одновременном действии касательных и нормальных напряжений

S = 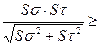[S] (4.10)

Обычно в расчётах принимают [S] ≥ 1,5

Рассмотренные условия прочности по допустимым напряжениям и коэффициенту запаса прочности взаимосвязаны:

[σ] = σ_разр ⁄ S (4.11)

Здесь σ_разр отражает технологию изготовления, режим нагружения и другие факторы.

Жёсткость -это способность деталей сопротивляться изменению их формы под действием нагрузок [2, 3, 13]. Для многих деталей (оси, валы, опоры подшипников и другие) расчёт на жёсткость является определяющим.

Значение критерия жёсткости постоянно возрастает, так как прочностные свойства материалов повышаются при практически неизменном модуле упругости.

Для оценки жёсткости деталей машин сравнивают наибольшие значения линейного f или углового φ перемещения или угла поворота θ с их допустимыми значениями:

- для линейного перемещения f_max ≤ [f] (4/12)

- для углового перемещения φ_max ≤[φ] (4.13)

- для угла поворота θ_max ≤[θ] (4.14)

Износостойкость– представляет собой сопротивляемость детали изнашиванию. Износ является одной из основных причин постепенных отказов деталей машин. Износ снижает долговечность деталей из-за снижения прочности деталей вследствие уменьшения сечений, неравномерного износа опор, увеличения динамических нагрузок (зубчатые колёса),возрастания шума в быстроходных передачах.

Расчёт на износостойкость выполняют обычно методами, сводящимися к определению размеров изнашиваемых поверхностей, обеспечивающих рабочее удельное давление ниже допустимого.

Метод расчёта по номинальным давлениям имеет экспериментальное и теоретическое обоснование в условиях малых перемещений, соответствующих зазорам в соединениях:

А_тр.= N_тр.·τ = р·w·τ = V ∕ K_и (4.15)

где N_тр - мощность трения, τ - время, р – удельное давление;

w – относительная скорость движения трущихся поверхностей; и V – объём истёртого материала; K_и - коэффициент износостойкости.

В расчете на основе теории подобия используют эмпирические степенные зависимости между контактным напряжением и износостойкостью, выраженные через путь трения S:

σ^m_конт. · S = const (4.16)

Здесь показатель степени m на основе эксперимента обычно колеблется от 1 до 3; меньшие значение – при сухом трении, большие – при работе со смазкой; в большинстве деталей и машин принимают около 3.

Теплостойкость– это свойство конструкции сохранять работоспособность в заданном температурном диапазоне.

Необходимость оценки теплостойкости машины (или узла) возникает при изменении температуры среды или при значительных потерях мощности, обусловленных интенсивным тепловыделением. Повышение температуры нагрева выше допустимой может привести к нарушению условий смазки, изменению механических свойств материалов и деформациям деталей.

От теплового режима существенно зависит работоспособность червячных и фрикционных передач, предохранительных муфт, тормозных устройств.

Обычно тепловые расчёты сводят к составлению уравнения теплового баланса вида : Q₁ = Q₂:

P·(1-η) = K·S(t₁ – t₂) (4.17)

где P – потребляемая мощность. Вт; η - КПД механизма; К – коэффициент теплопередачи Вт/м²·к; S – площадь охлаждаемой поверхности, м²; t₁ – температура смазки; t₂ – температура охлаждающей среды.

Выполнение условия (4.17) достигают увеличением охлаждающей поверхности корпуса машины; принудительным охлаждением сильно нагреваемых поверхностей и так далее. Тепловой режим необходимо учитывать при выборе материалов и размеров конструкций а также смазочного материала.

Виброустойчивость- это способность конструкции работать в условиях воздействия вибрации.

Повышение рабочих режимов машин и агрегатов часто способствует возникновению вибраций. Вибрационные нагрузки могут вызвать усталостное разрушение деталей, а при совпадении частоты собственных колебаний деталей с частотой внешних периодических сил наступает резонанс, приводящий к разрушению деталей или машины в целом. Помимо этого, колебания деталей зубчатых передач и их элементов вызывают повышенный шум.

С целью предотвращения колебаний изменяют динамические характеристики машины – моменты инерции масс и податливость соединений. При недостаточном эффекте этих мер в систему включают специальные устройства – виброгасители или антивибраторы (амортизаторы).

5. Конструктивные расчёты БМП

5.1 Расчёт механизмов на точность

Детали реальных механизмов отличаются от чертёжных образов наличием отклонений форм и размеров. Эти отклонения (погрешности) обусловлены действием разных причин как расчётного, так и производственного характера. Поэтому при проектировании необходимо учитывать влияние этих отклонений на точность движение механизма.

Разницу в положении ведомых звеньев действительного и теоретического механизмов при одинаковых положениях ведущих звеньев обоих механизмов называют ошибкой положения механизма, а разницу в их перемещениях – ошибкой перемещения механизма [1]

Первичной ошибкой механизма называют неточность геометрической формы, размеров и взаимного расположения элементов кинематических пар и звеньев в механизме.

Аналитический метод определения ошибок механизма.

Сущность метода заключается в составлении уравнения, в котором положение ведомого звена механизма X выражено в виде функции ряда параметров, влияющих на точность механизма: координат ведущего звена х₀, размеров х_1, положений звеньев х₂ и так далее:

х = f(х₀ , х_{1 ,} х₂ … х_n) = f(х_i) (5.1)

Функцию положения механизма можно составить, проектируя размеры звеньев на оси прямоугольной системы координат или используя соотношения размеров сторон и углов геометрических фигур, являющихся контурами механизма.

Для действительного (реального) механизма положение ведомого звена определяется уравнением:

х +Δх = f(х_i + Δх_i ) (5.2)

Раскладывая правую часть уравнения (5.2) в ряд Тейлора и ограничиваясь членами первого порядка ( ввиду малых значений первичных ошибок Δх_i ), получаем:

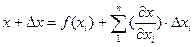(5.3)

где Δх =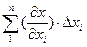

Таким образом, ошибка положения ведомого звена Δх равна сумме произведений первичных ошибок Δх_i на передаточные отношения для них (первые производные функций положения), При определении Δх допускают независимость действия первичных ошибок на ошибку Δх положения ведомого звена. Недостатком данного метода является его сложность. Графоаналитический метод определения ошибок механизма. Метод заключается в определении частных погрешностей механизма построением планов скоростей для некоторого преобразованного механизма. Преобразованный механизм получают закреплением ведущего звена действительного механизма в фиксированном положении, а звено, содержащее погрешность, превращают в ведущее звено другого механизма. При этом направление движения этого звена должно совпадать с направлением изменения параметра исследуемого звена. Рассмотрим применение этого метода на примере кривошипно-ползунного механизма (Рис.5.1)

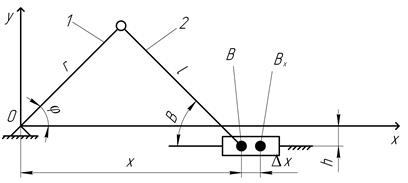
Рис. 5.1. Схема определения погрешности ведомого звена кривошипно-ползунного механизма.

1. Пусть ошибка в длине шатуна l будет Δl . Строим преобразованный механизм, при котором длина шатуна вследствие первичной ошибки Δl становится переменной. (Рис. 5.2а).

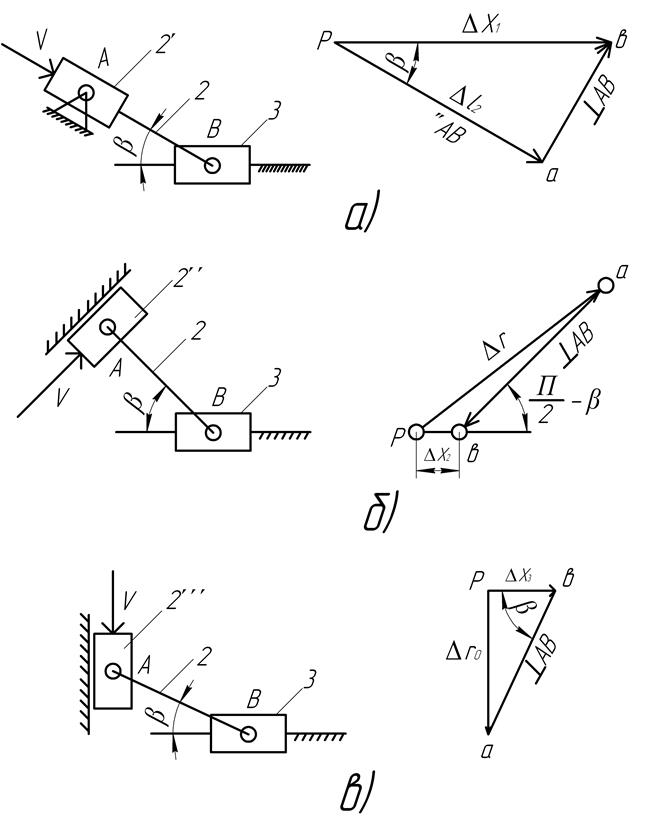
Рис 5.2

Схема преобразования механизма при

первичных ошибках: а – шатуна; б – кривошипа; в – в шарнире.

Строим в соответствующем масштабе план скоростей, учитывая, что V_В = V_А + V_АВ и находим ошибку положения ползуна Δх₁:

Δх₁ = Δl·P_b ⁄ Р_а (5.4)

2. Строим преобразованный механизм, в котором длина кривошипа вследствие первичной ошибки Δr стала переменной (Рис.5.2б)

Строим план скоростей для данного механизма и находим ошибку положения ползуна Δх₂

При этом

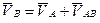
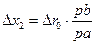(5.5)

3. Строим преобразованный механизм, в котором положение центра шарнира «0» от горизонтали вследствие первичной ошибки Δr₀ стало переменным (Рис.5.2в). При построении плана скоростей учитывается:

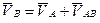
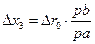(5.6)

Полная ошибка положения ползуна 3 в соответствующем масштабе равна алгебраической сумме ошибок звеньев:

Δx = Δx₁ + Δx ₂ + Δx₃ (5.7)

Изложенный метод определения погрешностей применим и для плоских механизмов с высшими кинематическими парами.

При проектировании механизмов необходимо учитывать систематические и случайные погрешности (первичные ошибки), являющиеся погрешностями производства.

Считая, что ошибка положения механизма подчиняется закону нормального распределения, предельные значения ошибок положения механизмов можно найти по формуле:

ε max = 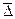x 3σx (5.8)

где Δx - величина средней ошибки положения механизма в результате всех первичных ошибок; σx - значение среднего квадратичного отклонения суммы независимых случайных ошибок Х_I.

5.2. Расчёт механизмов БМП на прочность.