Построение Коробовых кривых.

Коробовыми называются кривые, образованные сопряжением дуг окружностей. К коробовым кривым относят овалы, овоиды и т.п. Овал – замкнутая коробовая кривая, имеющая две оси симметрии. Строят овал по двум заданным осям – большой и малой, либо по одной большой оси.

· Построение овала по заданной большой оси АВ (рис. 2.56). Отрезок АВ делят на четыре равные части и получают центры сопряжений 0₁ и 0₂. Из центра 0 проводят дугу радиусом 0А до пересечения с вертикальной прямой в точках 0₃ и 0₄, получают линии центров. Из 0₁ радиусом R₁ = 0₁А проводят дугу окружности до пересечения в точках С и Е с линиями центров 0₁0₄ и 0₁0₃. Аналогично получают вторую пару точек сопряжения – D и F. Радиусом R = 0₄C проводят замыкающие дуги овала между точками С и D, E и F.

· Построение овала по двум осям АВ и СD (рис. 2.57). Соединяют прямой линией точки А и С. Радиусом большой полуоси АО засекают продолжение малой оси СD в точке К. Радиусом СК (разность полуосей) засекают линию АС в точке М. Проводят перпендикуляр через середину отрезка АМ, он пересекает оси овала в точках 0₁ и 0₄, которые являются искомыми центрами дуг окружностей. Центры 0₂ и 0₃ находят как точки симметричные центрам 0₁ и 0₄. Точки сопряжения 1, 2, 3 и 4 находятся на линиях центров соответственно 0₁0₄, 0₂0₄, 0₁0₃, и 0₂0₃. Строят овал как последовательность дуг окружностей: первая с центром 0₁ и радиусом R₁, вторая с центром 0₄ и радиусом R, третья с центром 0₂ и радиусом R₁, четвертая с центром 0₄ и радиусом R.

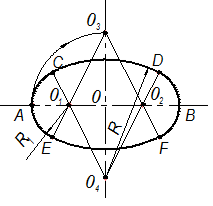Рис. 2.56

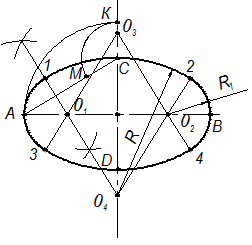Рис. 2.57

Овоид – замкнутая коробовая кривая, имеющая только одну ось симметрии. (яйцевидный овал). Его задают обычно радиусом или диаметром основной окружности.

· Построение овоида производится в следующей последовательности: Проводят линии центров А01 и В01. Радиусом АВ, равным диаметру заданной окружности, проводят дугу BD до линии центров А01, а радиусом R – дугу АС до линии центров В01. Замыкают овал дугой СD из центра 01.

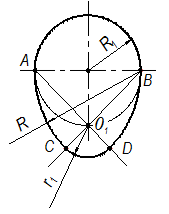Рис. 2.58