Метод середніх величин.
Середня величина ознаки визначається різними способами в залежності від об’єктів спостереження, ознак, що вивчаються, і методів вимірювання. В спортивній метрології існує декілька середніх величин: середня арифметична, мода, медіана, середня квадратична.
Середнє арифметичне – визначається як сума всіх значень вимірюваної ознаки, поділена на кількість значень суми. Для цього використовують формулу:
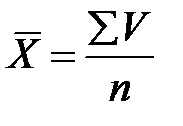 ,
,
де 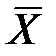 - середня арифметична;
- середня арифметична; 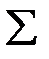 - знак сумації; V – варіанта статистичного ряду (вимірювана ознака у кожної особи досліджуваної групи).
- знак сумації; V – варіанта статистичного ряду (вимірювана ознака у кожної особи досліджуваної групи).
Наприклад: 5 хлопців пробігли дистанцію за 12,5; 13,0; 12,0; 11,6; 12,7 с.
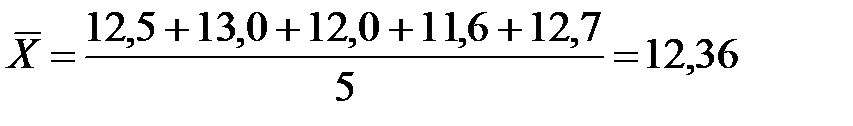 ,
,
На практиці використовують багато різних видів представлення статистичних даних. Найбільш часто вживають: текстовий вигляд; табличний вигляд; варіаційний ряд; графічний вигляд.
Якщо розрахунок відбувається в багато численній групі, тут найпопулярнішим методом статистики є метод складання варіаційного ряду, та здійснюється операцію ранжування – розташування чисел у порядку зростання чи зменшення.
Приклад У 43 легкоатлетів при виконанні старту з наступним бігом на 6 м виміряна величина стартової реакції (с):
| 1,28 | 1,30 | 1,38 | 1,32 | 1,32 | 1,36 | 1,40 | 1,30 |
| 1,38 | 1,30 | 1,40 | 1,32 | 1,41 | 1,42 | 1,38 | 1,32 |
| 1,41 | 1,28 | 1,32 | 1,28 | 1,30 | 1,32 | 1,30 | 1,40 |
| 1,32 | 1,32 | 1,30 | 1,42 | 1,41 | 1,40 | 1,32 |
Здійснюємо операцію ранжування:
| 1,28 | 1,28 | 1,28 | ||||||
| 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | ||
| 1,32 | 1,32 | 1,32 | 1,32 | 1,32 | 1,32 | 1,32 | 1,32 | 1,32 |
| 1,38 | 1,38 | 1,38 | ||||||
| 1,40 | 1,40 | 1,40 | 1,40 | |||||
| 1,41 | 1,41 | 1,41 | ||||||
| 1,42 | 1,42 |
Максимально спростимо ранжируваний матеріал, підрахуємо кількість кожного показника і вибудуємо їх у стовпці:
| xj | nj |
| 1,28 | |
| 1,30 | |
| 1,32 | |
| 1,38 | |
| 1,40 | |
| 1,41 | |
| 1,42 |
Отримана група чисел називається варіаційним рядом.
Варіаційний ряд – це подвійний стовпець ранжируваних чисел, де ліворуч стоїть власне показник – варіант, а праворуч – його кількість – частота. Сума частот називається об’ємом сукупності, тобто загальним числом вихідних даних. Сума всіх частот і являє собою обсяг сукупності.
Середня арифметична у цьому випадку знаходиться за формулою:
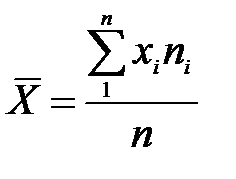 ,
,
де 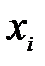 - варіанта ряду;
- варіанта ряду; 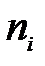 - частота ряду, n – об’єм сукупності.
- частота ряду, n – об’єм сукупності.
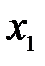
| 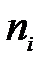
| 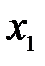 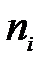
|
| 1,28 | 3,84 | |
| 1,30 | 9,10 | |
| 1,32 | 11,88 | |
| 1,38 | 4,14 | |
| 1,40 | 5,60 | |
| 1,41 | 4,23 | |
| 1,42 | 2,84 | |
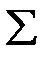
| 41,63 |
За формулою знаходимо:
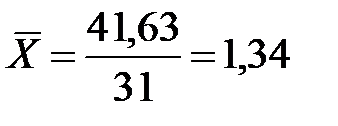
Дата добавления: 2015-09-07; просмотров: 2066;
