Нормировочная постоянная микроканонического распределения

В выражение для нормировочной постоянной (2.8)

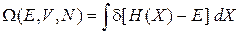
подставляем (2.10)

,

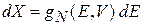­получаем

.

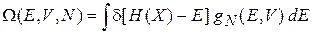Фильтрующее свойство дельта-функции снимает интеграл и дает

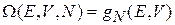. (2.11а)

Следовательно, нормировочная постоянная микроканонического распределения равна энергетической плотности состояний.