Теоретическое введение. Если из двух разнородных металлов образовать замкнутую цепь и контакты (спаи) металлов поддерживать при разных температурах

Если из двух разнородных металлов образовать замкнутую цепь и контакты (спаи) металлов поддерживать при разных температурах, то по цепи пойдёт ток. Это явление получило название термоэлектричества, а возникающая ЭДС – термоэлектродвижущей силы (ТЭДС). Термоэлектри‑
чество было открыто Зеебеком ещё в двадцатые годы XIX века.

В небольшом диапазоне температур величина ТЭДС

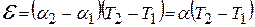. (15.1)

Здесь 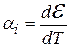– коэффициент Зеебека, характеризующий градиент потенциала, который возникает в проводнике, когда его концы поддерживаются при различных температурах. В неравномерно нагретом проводнике в отсутствие тока появляется электрическое поле. 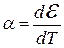– дифференциальная ТЭДС пары проводников, она зависит не только от рода данной пары проводников, но и от их состояния, в частности, от температуры; T₂ – температура одного из спаев, T₁ – температура другого (T₂ >T₁).

Величина дифференциальной ТЭДС для пары медь–платина при t=0⁰С равна, например, 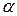=7.4^.10^-6 В/К.

Термоэлектричество широко используют для измерения температур. Для этого служат термоэлементы (термопары). Они содержат две проволоки из различных металлов, концы которых сварены (спай 1). Второй спай поддерживается при постоянной температуре T₁. Концы цепи присоединяют к милливольтметру. Измерив величину 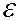и зная T₁ и 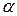, можно определить из (15.1) неизвестную температуру T₂ спая 1. Термопары обладают тем преимуществом, что позволяют измерить как очень высокие, так и очень низкие температуры, что невозможно сделать с помощью обычных жидкостных термометров.

ТЭДС обусловлена зависимостью внутренней контактной разности потенциалов от температуры в спае.

Причина появления контактной разности потенциалов между металлами 1 и 2 может быть понята на основе классических представлений об электронном газе в металлах, как об идеальном газе, давление которого определяется числом электронов в единице объема n и температурой Т.

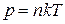, (15.2)

где k – постоянная Больцмана. Так что, если температуры обоих металлов одинаковы, но концентрации разные ( 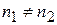), то давления электронного газа в этих металлах различны. Если, например, 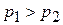, то электроны будут переходить из металла 1 в металл 2 в большем количестве, чем из 2 в 1 до тех пор, пока электрическое поле, возникающее вследствие преимущественного диффузионного перехода электронов, не компенсирует своим противодействием влияния перепада давления.

Внутреннюю контактную разность потенциалов 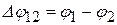легко оценить в рамках классической электронной теории. Задача о равновесии электронов в двух соприкасающихся проводниках не отличается от задачи о равновесии идеального газа в поле силы тяжести. В соответствии с классической статистикой, концентрация газа 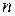на высоте 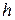связана с концентрацией 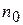у поверхности Земли распределением Больцмана

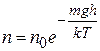, (15.3)

где m – масса молекулы газа, g=9.81 м/с².

В формуле (15.3) 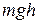есть разность потенциальных энергий 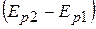молекулы газа на высоте 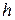и у поверхности Земли. Для двух соприкасающихся металлов 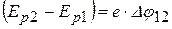и поэтому

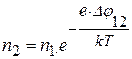. (15.4)

Отсюда получаем

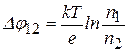. (15.5)

Из (15.5) следует, что чем больше различие в концентрациях электронов, тем больше и внутренняя контактная разность потенциалов. Оценим величину 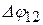. При комнатной температуре (Т=300 К) величина 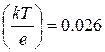В, величина же 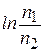порядка единицы. Поэтому 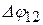получается порядка 10^-2÷10^-3 В, а 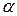соответственно порядка 10^-4 В/К, что примерно в 100 раз меньше величины, наблюдаемой на опыте.

Расхождение устраняется при использовании квантовой теории твёрдого тела. Количественное рассмотрение термоэлектрических эффектов будет иным – необходимо будет ввести понятие энергии Ферми для металлов и пользоваться квантовой статистикой, а не классической.