Теоретическое введение. В этой лабораторной работе рассмотрим, как простые модели металла могут быть использованы для объяснения термоэлектронной эмиссии электронов.
В этой лабораторной работе рассмотрим, как простые модели металла могут быть использованы для объяснения термоэлектронной эмиссии электронов.
Многие физические свойства металлов можно объяснить, основываясь на модели свободных электронов. В этой модели валентные электроны атомов металла считаются полностью свободными в пространстве, ограниченном поверхностью. Именно валентные электроны обуславливают электропроводность металла, и по этой причине их называют электронами проводимости и отличают от электронов, заполняющих оболочки ионных остовов.
Следующее доказательство правильности представления о свободных электронах в металлах мы обнаруживаем в явлениях термоэлектронной эмиссии. Известно (Ричардсон, 1903 г.), что электроны самопроизвольно выделяются из раскаленных металлов и что в отсутствие внешнего электрического поля они образуют электронное облако вокруг нагретого тела. Число таких электронов можно определить, измерив ток, возникающий при включении внешнего электрического поля.
Теоретически явление термоэлектронной эмиссии можно объяснить, используя модель свободных электронов. В металле электроны проводимости могут двигаться свободно, участвуя в тепловом движении. Так как они удерживаются внутри металла, то значит, вблизи поверхности металла существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Так как электрон – заряженная частица, то существование работы выхода показывает, что в поверхностном слое металла существует электрическое поле, а следовательно, электрический потенциал при переходе через этот поверхностный слой меняется на некоторую величину φ, которая, так же как и работа выхода, является характеристикой металла. Эта поверхностная разность потенциала связана с работой выхода очевидным соотношением:
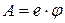, (13.1)
где e – заряд электрона.
Изменение потенциала внутри металла в отсутствие тока можно наглядно представить при помощи диаграммы (рис.13.1). По вертикальной оси отложена потенциальная энергия электрона Ep, то есть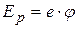 
, причём значение потенциала вне металла принято равным нулю. Потенциальная энергия электрона вне металла постоянна; в поверхностном слое она быстро изменяется, а именно уменьшается на величину работы выхода, а внутри металла опять становится постоянной. Так что распределение потенциальной энергии электрона внутри металла представляется в виде потенциальной ямы (ящика).
Можно указать две причины возникновения работы выхода. Одна заключается в индукционном действии удаляемого электрона из металла. Такой электрон вызывает на поверхности металла положительный индуцированный заряд, отчего между электронами и металлом возникает сила притяжения, препятствующая удалению электрона. Вторая заключается в том, что вылетевшие из металла электроны образуют электронное облако. В результате у поверхности металла возникает тонкий двойной электрический слой, электрическое поле которого препятствует вылету электронов из металла.
Если электрон внутри металла имеет кинетическую энергию Eк1 меньшую, чем глубина потенциального ящика (рис.13.1):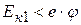 
, то такой электрон не сможет покинуть металл. Если же его кинетическая энергия 
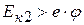, то электрон вылетает из металла. Условия вылета электрона из металла:
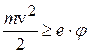, (13.2)
где m – масса электрона, v – его скорость.
Работа выхода для металлов имеет порядок нескольких электрон-вольт (1 эВ=1.6.10-19 Дж). Величина энергии теплового движения равна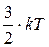 
, и при комнатной температуре Т=300 К она равна 0.02 эВ (то есть 
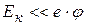). Поэтому при комнатной температуре подавляющее большинство электронов проводимости находится внутри металла.
Зависимость плотности тока насыщения jн (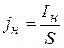 
) от температуры катода Т известна в литературе под названием формулы Ричардсона-Дэшмена:
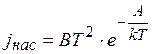, (13.3)
где k – постоянная Больцмана, равная 1.38.10-23 Дж/К; В – постоянная, величина которой для многих чистых металлов лежит в пределах: (0.6÷162)А/(м2.К2).
Рассмотрим, как классическая статистическая физика объясняет эту зависимость. Термоэлектронная эмиссия заключается в том, что быстрые электроны металла, обладающие кинетической энергией теплового движения, большей, чем работа выхода, встречая поверхность металла, преодолевают потенциальный барьер на поверхности и выходят за пределы металла. Для этого надо найти число электронов, ударяющихся за секунду о единицу поверхности металла и причем таких, у которых кинетическая энергия перпендикулярной к поверхности составляющей скорости движения, например по оси ОХ, достаточна для преодоления потенциального барьера. Если обозначим через n1 число таких электронов, то
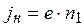. (13.4)
Далее, используя закон распределения Максвелла по скоростям, нужно найти число электронов, для которых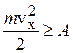 
. Число электронов n в единице объема, скорость которых лежит в интервале скоростей между v и (v+dv), равно (распределение Максвелла)
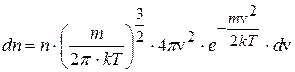. (13.5)
Аналогично число электронов в единице объема с компонентой скорости между vx и (v x+dvx) равно
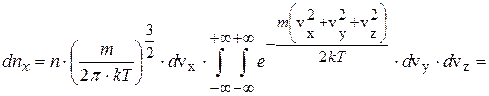
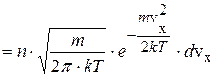, (13.6)
поскольку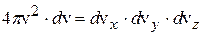 
, 
.
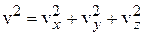Теперь, чтобы получить число таких электронов, попадающих на единичную площадку поверхности металла за одну секунду, нужно величину dnx умножить на vx, так как за единицу времени поверхности достигают все электроны с компонентой скорости vx, содержащиеся в слое толщины vx, прилегающем к поверхности. Таким образом, плотность тока насыщения выражается интегралом
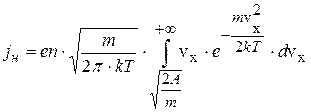. (13.7)
Взяв этот интеграл, получим выражение
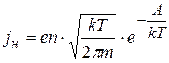. (13.8)
Этот результат основан на представлениях классической электронной теории.
Квантовая теория металлов, в которой распределение электронов проводимости по энергиям – это распределение Ферми, приводит к соотношению (13.3), в которое вместо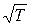 
в (13.8) входит 
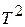. Нужно заметить, что на опыте это различие не очень существенно, так как зависимость 
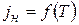определяется главным образом экспоненциальным множителем 
.
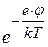Дата добавления: 2015-09-07; просмотров: 541;