Теоретическое введение. Случайная величина. Понятие о статистическом распределении.
Случайная величина. Понятие о статистическом распределении.
В научных исследованиях, технике и массовом производстве часто приходится встречаться с особого типа явлениями, которые принято называть случайными. Случайное явление – это явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному. Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.
В природе нет ни одного физического явления, в котором не присутствовал бы в той или иной мере элемент случайности. Как бы точно ни были фиксированы условия опыта, невозможно достигнуть полного и точного совпадения результатов при повторении опыта. Существуют такие задачи, где исход опыта зависит от столь большого числа факторов, что практически невозможно зарегистрировать и учесть их все. Однако если обратиться к совокупности большого числа явлений, то средние результаты обнаруживают устойчивые закономерности, свойственные именно массовым случайным явлениям. Примерами такого рода законов могут служить распределения молекул по скоростям (закон Максвелла) и по компонентам скоростей (описывается функцией Гаусса).
Случайная величина называется дискретной, если она принимает счетное множество значений,например, число молекул в выделенном объеме газа, энергия электрона в атоме, число зерен в колосьях. Непрерывная случайная величина принимает любые значения внутри некоторого интервала: координата материальной точки, температура воздуха, масса зерен в колосьях.
Элементы классической статистики.
Пусть имеется макросистема, то есть система, состоящая из большого числа микрочастиц. Пусть какая-либо случайная дискретная величина х может принимать значения х1, х2, х3,…. Произведем N измерений величины х, приводя систему каждый раз перед измерением в одно и то же состояние. Вместо того, чтобы производить N измерений над одной системой, можно взять N одинаковых систем и измерять величину х один раз в каждой системе. Статистический ансамбль – это набор одинаковых систем, находящихся в одинаковом состоянии. Пусть при измерениях х значение х1 получено в N1 измерениях, значение х2 – в N2 измерениях и т.д. Очевидно,
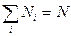 . (11.1)
. (11.1)
Вероятность pi (или р(хi)) появления результата хi – это 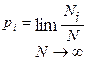 , причем из (11.1) следует условие нормировки (11.2):
, причем из (11.1) следует условие нормировки (11.2):
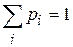 . (11.2)
. (11.2)
Из определения вероятности следует, что 0≤р≤1, причем р=0 для невозможного события и р=1 для достоверного события.
Два событиянесовместны,если их одновременное осуществление невозможно (например, выпадение 1 и 3 при однократном бросании кости). Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления второго. Математическая вероятность подчиняется определенным закономерностям.
Закон сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей. То есть, вероятность р(хi или хj) получить результат хi или хj равна сумме их вероятностей:
р(хi или хj)= р(хi)+ р(хj). (11.3)
Например, вероятность выпадения четного числа при однократном бросании игральной кости р(2 или 4 или 6)=р(2)+р(4)+р(6)=1/6+1/6+1/6=1/2.
Закон умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей.
р(хi и хj)= р(хi) р(хj). (11.4)
Например, при бросании двух игральных костей вероятность получить сумму чисел на гранях 12 равна р(6 и 6)= 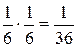 .
.
Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, или числовые характеристики случайной величины. Это – математическое ожидание М, дисперсия D и среднее квадратическое отклонение σ.Среднее арифметическое значение 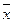 дискретной случайной величины
дискретной случайной величины
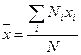 (11.5)
(11.5)
при большом числе измерений (N→∞) стремится к математическому ожиданию
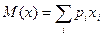 . (11.6)
. (11.6)
Возможные значения дискретной случайной величины рассеяны вокруг ее математического ожидания, часть их превышает M(x), часть – меньше M(x). Дисперсия характеризует «разбросанность» случайной величины вокруг математического ожидания.
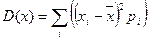 (11.7)
(11.7)
Среднее квадратическое отклонение, по определению:
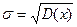 . (11.8)
. (11.8)
Непрерывную случайную величину нельзя задать тем же законом распределения, что и дискретную. Введем f(x) – функцию распределения вероятностей случайной величины – следующим образом.
Пусть dP – вероятность того, что непрерывная случайная величина принимает значения в интервале от x до x+dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP прямо пропорциональна dx. Кроме того, вероятность должна зависеть и от самой случайной величины x, вблизи которой расположен интервал, поэтому
dP= f(x)dx, (11.9)
где f(x) – плотность вероятности, т.е. функция, показывающая, как изменяется вероятность, отнесенная к интервалу dx случайной величины, от значения самой этой величины:
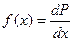 (11.10)
(11.10)
Вероятность того, что случайная величина принимает какое-либо значение в интервале от a до b, получается интегрированием функции:
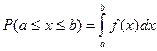 (11.11)
(11.11)
Условие нормировки для непрерывной случайной величины имеет вид:
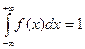 . (11.12)
. (11.12)
Замечание к формуле (11.12): интегрирование должно производиться по всей области определения функции.
Для непрерывной случайной величины математическое ожидание M(x) (среднее значение х) и дисперсия D(x) записываются соответственно в виде:
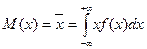 , (11.13)
, (11.13)
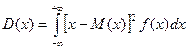 , (11.14)
, (11.14)
а среднее значение любой функции φ(х) равно:
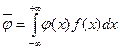 . (11.15)
. (11.15)
Нормальный закон распределения (закон Гаусса)
Существуют различные виды распределения случайных величин. Однако особое значение в теории вероятностей и в различных практических приложениях имеет нормальный закон распределения (закон Гаусса), характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным. Закон Гаусса применяют, если выполняются следующие требования:
1. Величина может принимать непрерывный ряд значений.
2. При большом числе наблюдений отклонения от среднего одинаковой величины, но разного знака встречаются одинаково часто.
3. Большие отклонения от среднего встречаются реже, чем малые.
Плотность вероятности для нормального закона распределения описывается формулой:
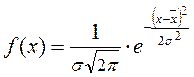 , (11.16)
, (11.16)
где 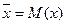 – математическое ожидание случайной величины, σ – среднее квадратическое отклонение.
– математическое ожидание случайной величины, σ – среднее квадратическое отклонение.
Кривая нормального закона распределения имеет колоколообразную форму (рис.11.1), симметричную относительно вертикальной прямой x= 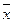 . С уменьшением σ кривая становится все более островершинной. Площадь, заключенная под всей кривой, согласно условию нормировки (11.12), равна единице.
. С уменьшением σ кривая становится все более островершинной. Площадь, заключенная под всей кривой, согласно условию нормировки (11.12), равна единице.
Удобно привести функцию Гаусса (11.16) к виду (11.17), если ввести безразмерную переменную 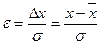 :
:
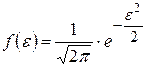 . (11.17)
. (11.17)
Тогда вероятность того, что х отклоняется от 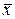 не больше, чем на Δх, можно рассчитать так:
не больше, чем на Δх, можно рассчитать так:
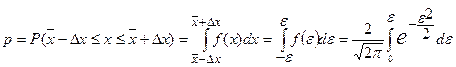 . (11.18)
. (11.18)
Результаты вычисления р по формуле (11.18) приведены в табл. 11.1.
Таблица 11.1
| e | р | e | р | e | р |
| 0.4 | 0.31 | 2.0 | 0.95 | ||
| 0.1 | 0.08 | 0.5 | 0.38 | 2.5 | 0.988 |
| 0.2 | 0.16 | 1.0 | 0.68 | 3.0 | 0.997 |
| 0.3 | 0.24 | 1.5 | 0.87 | 4.0 | 0.99993 |
Очевидно, чем больше Δх, то есть чем больше ε, тем больше вероятность того, что случайная величина принимает значение в интервале от 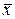 –Δх до
–Δх до 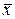 +Δх. Так, например, вероятность того, что случайная величина принимает какое-либо значение в интервале от
+Δх. Так, например, вероятность того, что случайная величина принимает какое-либо значение в интервале от 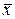 –σ до
–σ до 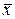 +σ (ε=1), из (11.11):
+σ (ε=1), из (11.11):
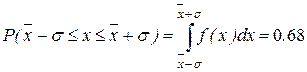 ,
,
 то есть заштрихованная на рис.11.1 площадь равна 0.68. Если ε=2, то вероятность того, что случайная величина отклоняется от среднего значения
то есть заштрихованная на рис.11.1 площадь равна 0.68. Если ε=2, то вероятность того, что случайная величина отклоняется от среднего значения 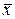 (математического ожидания) не больше, чем на Δх=2σ, равна 95%, а отклонение случайной величины на Δх=3σ (ε=3) происходит с вероятностью 99.7%.
(математического ожидания) не больше, чем на Δх=2σ, равна 95%, а отклонение случайной величины на Δх=3σ (ε=3) происходит с вероятностью 99.7%.
Закону Гаусса подчиняется распределение молекул газа по компонентам скоростей. Если газ находится в состоянии равновесия, в нем устанавливаются постоянные давление и температура. При этом молекулы газа движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Несмотря на полную хаотичность молекулярных движений, их распределение по скоростям оказывается вполне определенным, если число молекул газа достаточно велико. На характер распределения не влияют ни столкновения между молекулами, ни внешние поля. Оно оказывается однозначным и единственно возможным.
Как бы ни изменялись скорости различных молекул, среднее значение квадрата скорости остается постоянным и равно
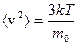 , (11.19)
, (11.19)
где m0 – масса молекулы, Т – термодинамическая температура газа, k – постоянная Больцмана. Введём функцию распределения по компонентам скоростей: j(vx)dvx= 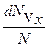 – доля молекул, проекции скорости которых на ось ОХ лежат в интервале от vх до vх+dvх. Хаотичность движения молекул позволяет принять для проекции скорости vх молекулы нормальный закон распределения. Как показал Д.К.Максвелл, плотность вероятности того, что молекула имеет компоненту скорости vх, равна:
– доля молекул, проекции скорости которых на ось ОХ лежат в интервале от vх до vх+dvх. Хаотичность движения молекул позволяет принять для проекции скорости vх молекулы нормальный закон распределения. Как показал Д.К.Максвелл, плотность вероятности того, что молекула имеет компоненту скорости vх, равна:
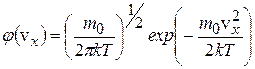 , (11.20)
, (11.20)
 График функции распределения по компонентам скоростей изображен на рис.11.2.
График функции распределения по компонентам скоростей изображен на рис.11.2.
Функция принимает максимальное значение при vx=0 и симметрична относительно оси ординат. Это значит, что среднее значение проекции скорости и ее наиболее вероятное значения равны нулю. Доля молекул, движущихся в данный момент времени в плоскости, перпендикулярной оси ОХ, максимальна.
Поскольку все направления движения молекул в пространстве равноправны, выражения для j(vy) и j(vz) аналогичны выражению (11.20). Вероятность того, что молекула имеет проекцию скорости, лежащую в интервале от vх до vх+dvх:
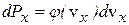 . (11.21)
. (11.21)
Дата добавления: 2015-09-07; просмотров: 1097;
