ВОЛНОВАЯ функция
Состояние частицы описывается комплексной функцией
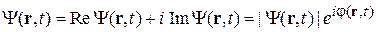 ,
,
являющейся амплитудой вероятности обнаружения частицы. Квадрат модуля волновой функции
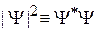
равен плотности вероятности, то есть вероятности обнаружения частицы в момент t в единичном объеме около точки r
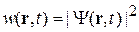 .
.
Вероятность обнаружения частицы в момент t в объеме 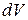 около точки
около точки 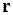 равна
равна
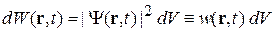 .
.
Выполняется нормировка вероятности
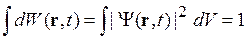 .
.
Шредингер назвал волновую функцию «каталогом информации» о всевозможных результатах экспериментов с частицей.
Волновая функция:
1) Квадратично интегрируема, т. е. существует 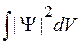 ;
;
2) Удовлетворяет принципу суперпозиции – если возможны состояния  и
и  , то возможно состояние
, то возможно состояние
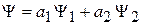 ,
,
где 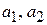 – комплексные числа, определяющие вероятность обнаружения состояния 1 или 2;
– комплексные числа, определяющие вероятность обнаружения состояния 1 или 2;
3) Функция определена не полностью, остается произвол в выборе постоянного фазового множителя. Состояния  и
и 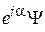 , где
, где 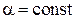 , физически не различимы, плотность вероятности для них одинакова
, физически не различимы, плотность вероятности для них одинакова 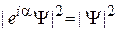 .
.
Дата добавления: 2015-09-21; просмотров: 605;
