И собственные значения операторА
Собственная функция 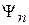 оператора
оператора 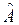 определяется уравнением
определяется уравнением
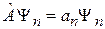 , (2.8)
, (2.8)
где 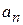 – собственное значение оператора для функции
– собственное значение оператора для функции 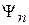 . Под действием оператора его собственная функция восстанавливается с точностью до постоянного множителя, который называется собственным значением.
. Под действием оператора его собственная функция восстанавливается с точностью до постоянного множителя, который называется собственным значением.
Физический смысл собственного значения – если система находится в состоянии 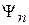 , то измерение величины A, описываемой оператором
, то измерение величины A, описываемой оператором 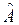 , дает однозначный результат
, дает однозначный результат 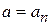 . Собственные функции с разными собственными значениями взаимно ортогональны. Это исключает возможность получить при измерении неоднозначный результат.
. Собственные функции с разными собственными значениями взаимно ортогональны. Это исключает возможность получить при измерении неоднозначный результат.
Спектр оператора – это множество его собственных значений 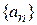 . Если
. Если 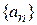 счетное, то спектр дискретный. Если
счетное, то спектр дискретный. Если 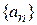 образует непрерывный набор, то спектр непрерывный. Возможен смешанный спектр – в одной области собственных значений один тип, в примыкающей области другой тип спектра.
образует непрерывный набор, то спектр непрерывный. Возможен смешанный спектр – в одной области собственных значений один тип, в примыкающей области другой тип спектра.
Если k разных собственных функций имеют одинаковые собственные значения, то спектр k-кратно вырожден.
Множество собственных функций 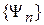 оператора
оператора 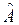 образует полный ортонормированный базис. Произвольное состояние частицы Ψ разлагается по этому базису
образует полный ортонормированный базис. Произвольное состояние частицы Ψ разлагается по этому базису
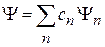 .
.
Как показано далее, коэффициент разложения 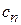 является амплитудой вероятности, тогда
является амплитудой вероятности, тогда  – вероятность результата
– вероятность результата 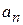 при измерении величины A в состоянии Ψ. Измерение проектирует состояние Ψ на орты базиса
при измерении величины A в состоянии Ψ. Измерение проектирует состояние Ψ на орты базиса 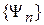 , проекция
, проекция 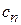 является амплитудой вероятности результата.
является амплитудой вероятности результата.
Коммутирующие операторы имеют одинаковый набор собственных функций, соответствующие физические величины одновременно имеют определенные значения.
Доказательство:
Пусть 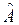 и
и 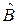 – взаимно коммутирующие операторы,
– взаимно коммутирующие операторы, 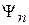 – собственная функция
– собственная функция 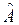 , тогда
, тогда
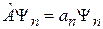 .
.
Действуем оператором 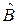 на обе стороны равенства
на обе стороны равенства
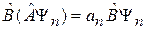 .
.
Учитываем коммутативность операторов
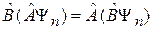 ,
,
получаем
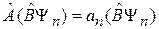 .
.
Следовательно, 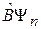 – собственная функция
– собственная функция 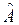 с собственным значением
с собственным значением 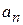 , поэтому она пропорциональная
, поэтому она пропорциональная 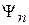
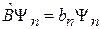 .
.
Полученное равенство означает, что 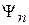 – собственная функция не только для
– собственная функция не только для 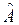 , но и для
, но и для 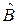 с собственным значением
с собственным значением 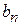 .
.
Дата добавления: 2015-09-21; просмотров: 1376;
