Средняя концентрация фотонов
Согласно (1.2)
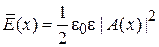
средняя энергия единицы объема волны пропорциональна квадрату модуля волны
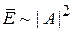 .
.
Энергия фотона (1.6)
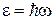 ,
,
тогда средняя концентрация фотонов
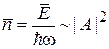 .
.
Если в объеме имеется один фотон, то вместо концентрации используется плотность вероятности – вероятность обнаружения фотона в единице объема. В результате плотность вероятности обнаружения фотона пропорциональна квадрату модуля волны
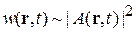 . (1.10)
. (1.10)
Волна де Бройля
Корпускулярно-волновая двойственность согласно де Бройлю присуща не только фотону, но и частице вещества.
По аналогии с фотоном частицу вещества описываем волной. Используя (1.8)
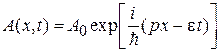 ,
,
получаем, что частице массой m, движущейся вдоль оси x в поле с потенциальной энергией 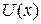 и с полной энергией Е сопоставляется волна де Бройля, или волновая функция (обозначаемая греч. буквой «пси»):
и с полной энергией Е сопоставляется волна де Бройля, или волновая функция (обозначаемая греч. буквой «пси»):
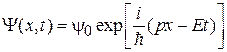 , (1.11)
, (1.11)
где
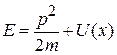 – полная энергия частицы,
– полная энергия частицы,
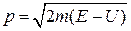 – модуль импульса частицы.
– модуль импульса частицы.
Длина волны
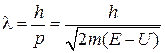 . (1.13)
. (1.13)
Чем больше энергия, тем меньше длина волны. Для электрона с энергией в пределах от 1 эВ до 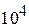 эВ длина волны лежит в пределах от ~ 1 нм до
эВ длина волны лежит в пределах от ~ 1 нм до 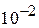 нм. В металлах длина волны де Бройля носителя тока порядка нанометра, в полупроводниках – несколько микрометров. Столь маленькая длина волны проявляется при дифракции и интерференции на объектах микроскопического размера.
нм. В металлах длина волны де Бройля носителя тока порядка нанометра, в полупроводниках – несколько микрометров. Столь маленькая длина волны проявляется при дифракции и интерференции на объектах микроскопического размера.
Плотность вероятности обнаружения частицы
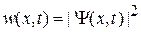 , (1.14)
, (1.14)
т. е. вероятность найти частицу в момент t в единичном интервале около точки x. Вероятность обнаружения частицы в интервале dx
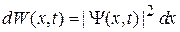 . (1.15)
. (1.15)
Вероятность найти частицу во всем пространстве равна единице и выполняется условие нормировки
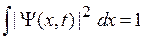 . (1.16)
. (1.16)
Квантование Бора–Зоммерфельда
При распространении микрочастицы по траектории условие максимума интерференции (1.3)
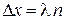
обеспечивает наибольшую амплитуду волны и наибольшую вероятность обнаружения частицы, движущейся между начальной и конечной точками двумя путями, отличающимися по длине на 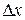 .
.
Рассмотрим движение частицы с постоянным модулем импульса p по замкнутой траектории длиной 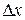 . Частица выходит из некоторой точки траектории и приходит в другую точку двумя путями. Один путь является кратчайшим, на втором пути частица делает лишний полный оборот по траектории, что превышает первый путь на длину траектории
. Частица выходит из некоторой точки траектории и приходит в другую точку двумя путями. Один путь является кратчайшим, на втором пути частица делает лишний полный оборот по траектории, что превышает первый путь на длину траектории 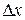 . Используя (1.13)
. Используя (1.13)
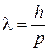 ,
,
получаем условие обнаружения частицы на траектории
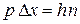 .
.
Нарушение этого условия приводит к резкому уменьшению амплитуды волны и вероятности обнаружения частицы.
Обобщаем результат на случай, когда импульс изменяется вдоль траектории с элементом 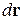 , и получаем формулу квантования Бора–Зоммерфельда
, и получаем формулу квантования Бора–Зоммерфельда
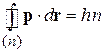 , (1.17)
, (1.17)
где
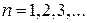 – квантовое число, или номер траектории, показывает число раз, которое длина волны де Бройля укладывается на протяжении траектории;
– квантовое число, или номер траектории, показывает число раз, которое длина волны де Бройля укладывается на протяжении траектории;
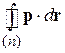 – объем фазового пространства
– объем фазового пространства 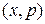 одномерного движения, занятого n состояниями. Следовательно, каждое квантовое состояние одномерного движения занимает в фазовом пространстве объем, равный h.
одномерного движения, занятого n состояниями. Следовательно, каждое квантовое состояние одномерного движения занимает в фазовом пространстве объем, равный h.
Формула (1.17) применимав квазиклассическом приближении, когда существует траектория частицы, т. е. длина волны де Бройля гораздо меньше характерного размера траектории r. С учетом и (1.17) и (1.13)
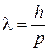 ,
,
получаем условия применимости (1.17)
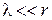 ,
, 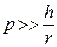 ,
, 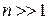 . (1.18)
. (1.18)
Полуклассическая теория неприменима для системы с характерным размером, сравнимым с длиной волны де Бройля, когда отсутствует понятие траектории.
Дата добавления: 2015-09-21; просмотров: 1408;
