V Пример. Дихотомическое деление. В содержании понятия «логика» (А) в качестве основания для деления возьмём признак «являться классической»

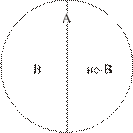
Дихотомическое деление. В содержании понятия «логика» (А) в качестве основания для деления возьмём признак «являться классической». Соответственно, выделим в объёме делимого понятия (А) подмножество тех элементов (В), которые обладают данным признаком, и подмножество тех элементов (не-В), которые не обладают данным признаком. Таким образом, в объёме делимого понятия оказались выявлены два подкласса, соответствующие противоречащим понятиям «классическая логика» (В) и «неклассическая логика» (не-В). Схема данного деления изображена слева.

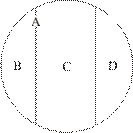
Деление по видообразующему признаку,Треугольники (А) по признаку (основанию деления) «величина угла» подразделяются на 3-и множества: 1) прямоуголь­ные (В), 3) тупоугольные (С) и 3) остроугольные (D) (рис. 9).

Рис.9

Классификация. Имеет место в случае последовательного деления понятия, образующего развёрнутую с относительно устойчивым характером и познавательно значимую систему, в которой её члены подразделёны на подвиды вплоть до одноэлементного понятия. К классификации может приводить как дихотомическое деление понятия, так и деление понятия по видообразующему признаку.