Формула Эйлера для числа вершин, ребер и граней плоского графа

Формула Эйлера связывает число вершин и ребер плоского графа с числом его граней. Гранью называется область плоскости, ограниченная ребрами плоского графа, не содержащая внутри себя ни ребер, ни вершин.

Итак, формула Эйлера:

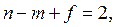
где n – число вершин, m – число ребер графа, f – число граней графа.

Исходя из этой формулы, был сформулирован ряд следствий:

Следствие 1. В любом простом планарном графе существует вершина, степень которой не больше пяти.

Следствие 2. Каждый планарный граф G с n ≥ 4 вершинами имеет, по крайней мере, четыре вершины со степенями, не превышающими 5.

Следствие 3. Если G – связный простой планарный граф с n ≥ 3 вершинами и m ребрами, то m ≤ 3n – 6.

Приведенные следствия определяют зависимость планарности графа от числа его вершин и ребер и задают границы интервала по числу ребер, при попадании в который необходимо проводить дополнительные исследования, чтобы получить достоверный ответ на вопрос, является ли планарным исследуемый граф.