Изоморфные графы

Граф G (рис. 1) можно изображать по-разному. Во-первых, не обязательно изображать его ребра прямолинейными. Можно провести любые линии, соединяющие те же самые вершины, что ираньше, так что граф G можно представить в виде, изображенном на рис. 7.

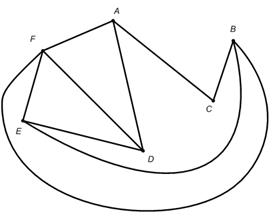
Рис. 7. Граф G₁, изоморфный графу G, изображенному на рис. 1

Во-вторых, можно произвольно располагать вершины на плоскости. Например, вершины графа Gможно расположить так, как показано на рис.8.

Если рассматривать три графа, изображенные нарис. 1, 7 и 8, как графы, описывающие ход спортивного турнира, то они будут содержать в точности одну и ту же информацию относительно того, какие именно команды уже играли друг с другом; в некотором смысле это один и тот же граф. Мы будем говорить, что два графа – обозначим их G₁ и G₂ – изоморфны, если они отвечают одному и тому же списку проведенных игр. Иными словами, если графы G₁ и G₂ изоморфны, то они имеют одно и то же число вершин и для любых двух вершин графа G₁ , скажем В₁ и С₁, соединенных ребром, соответствующие им вершины В₂ и С₂ графа G₂ тоже соединены ребром, и обратно.

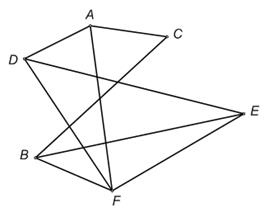
Рис. 8. Граф G₂, изоморфный графу G, изображенному на рис. 1 и графу G₁, изображенному на рис. 7

Согласно этому определению, три графа на рис. 1, 7 и 8 изоморфны (т. е. имеют одно и то же строение), хотя они и выглядят по-разному. (Термин «изоморфный» часто используется в математике; он состоит из греческих слов ιζωσ (isos) – равный, одинаковый и μορφε (morphē) – вид, форма).

Нередко приходится решать вопрос о том, являются ли два данных графа изоморфными. Иногда сразу ясно, что это не так. Например, графы, изображенные на рис. 9, не могут быть изоморфными, потому что они имеют неодинаковое число вершин.

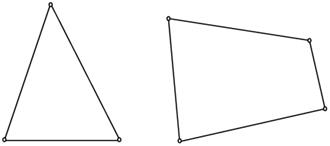
Рис. 9. Пример неизоморфных графов

Не могут быть изоморфными и графы рис. 10, так как у них неодинаковое число ребер.

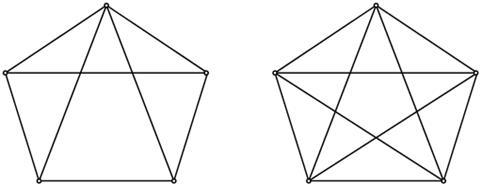
Рис. 10. Пример неизоморфных графов

Однако для того, чтобы показать, что не изоморфны графы, изображенные на рис. 11, требуется уже несколько более тонкое рассуждение.

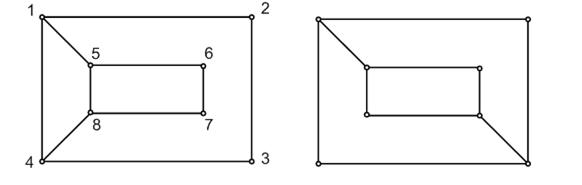
Рис. 11. Менее очевидный пример неизоморфных графов

Так, можно заметить, что на первом графе имеется последовательность из восьми смежных ребер (т. е. ребер, попарно имеющих общую вершину):

(1,2), (2,3), (3,4), (4,8), (8,7), (7,6), (6,5), (5,1),

возвращающаяся к исходной вершине, в то время как на втором графе такой последовательности нет. Значит, как бы ни были обозначены вершины второго графа, невозможно для каждой пары соединенных ребром вершин одного графа указать во втором соответствующую пару вершин, тоже соединенных ребром. (Докажите это!)

Если сразу не видно, как доказать, что два графа не изоморфны, то вопрос об их изоморфности может оказаться довольно трудным.

Рис. 12. Пример неочевидного изоморфизма графов

В качестве примера рассмотрим два графа, изображенных на рис. 12; эти графы на самом деле изоморфны.