Неориентированные графы.
Иногда граф рассматривают без учета ориентации дуг, тогда его называют неориентированным графом. Понятие “дуга”, “путь” и “контур" для неориентированного графа заменяются понятиями “ребро”, “цепь”, “цикл”. Ребро - это отрезок, соединяющий 2 вершины. Цепь - последовательность ребер. Цикл - цепь, у которой начальная и конечная вершины совпадают. Описать неориентированный граф можно путем задания пары множеств (Х,U), где Х - множество вершин; U - множество ребер. Однако более удобным является описание неориентированного графа с помощью матрицы смежности или инцидентности, которые строятся аналогично соответствующим матрицам для ориентированных графов с той разницей, что не делается различия между заходящей в вершину и исходящей из нее дугами. При этом вершины х и y называют смежными, если существует соединяющее их ребро, а само это ребро называется инцидентным вершинам х и у.
Укажем еще несколько определений, служащих для характеристики неориентированных графов.
Степенью вершины х, обозначаемой deg(x) или dx, называют число ребер, инцидентных вершине х. Так для графа на рис.2.4 имеем d1=2, d2=2, d3=3, d4=1, d5=0. Если dx=1, то вершину называют тупиковой; если dx=0 то вершину называют изолированной.
Теорема. Пусть G - неориентированный граф с n вершинами и m ребрами и dj - степень j-й вершины тогда Snj=1 dj=2m.
Доказательство теоремы следует из того, что каждое ребро добавляет 1-цу к степени каждой из 2-х вершин, которые оно соединяет, т.е. добавляет 2 к сумме степеней уже имеющихся вершин.
Следствие. В каждом графе число вершин нечетной степени четно.
Для неориентированного графа понятия “подграф” и “частичный граф” аналогичны соответствующим понятиям для ориентированного графа.
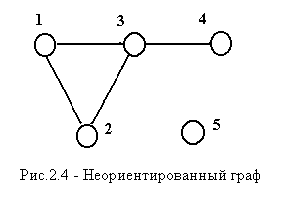 С понятием неориентированного графа связана важная характеристика, называемая связностью графа. Говорят, что граф связен, если любые две его вершины можно соединить цепью. Если граф G не связен, то его можно разбить на такие подграфы Gi, что все вершины в каждом подграфе связны, а вершины из различных подграфов не связны. Такие подграфы Gi называют компонентами связности графа G. Если из графа (рис.2.4) исключить изолированную вершину 5, то полученный граф будет связным. Граф на рис.2.5 не связен и имеет две компоненты связности.
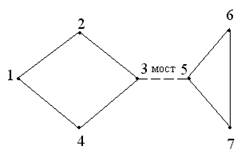
С понятием неориентированного графа связана важная характеристика, называемая связностью графа. Говорят, что граф связен, если любые две его вершины можно соединить цепью. Если граф G не связен, то его можно разбить на такие подграфы Gi, что все вершины в каждом подграфе связны, а вершины из различных подграфов не связны. Такие подграфы Gi называют компонентами связности графа G. Если из графа (рис.2.4) исключить изолированную вершину 5, то полученный граф будет связным. Граф на рис.2.5 не связен и имеет две компоненты связности.
|
Его можно превратить в связный, добавив ребро (мост), соединяющее вершины 3 и 5 (штриховая линия). Удаление моста превращает связной граф в несвязный.
Для того чтобы определить связность ориентированного графа не нужно обращать внимание на ориентацию дуг. Граф, изображенный на рис.1 является не связным.
Рис.2.5- Несвязный граф.
 Рис.2.6 - Граф в форме дерева
Рис.2.6 - Граф в форме дерева
|
Однако его подграф, состоящий из вершин b,c,d,e является связным. Для ориентированного графа существует понятие сильной связности. Граф сильно связан, если для любых 2-х вершин (х и у, х¹у) существует путь, идущий из х в у. Важный частный случай неориентированного графа - дерево. (рис.2.6) Деревом называют конечный связный неориентированный граф, не имеющий циклов. Если дано множество вершин a,b,c,..., то дерево можно построить следующим образом. Одной из вершин например а, примем за начальную и назовем его корнем дерева. Из этой вершины проводим ребра в близлежащие вершины b, c, d,... из них проводим рёбра в соседние с ними вершины c, f, g, h,... и т.д. Т.о. дерево можно построить последовательно добавляя рёбра в его вершинах. Это даёт возможность установить связь между числом вершин и числом рёбер дерева. Простейшее дерево состоит из 2-х вершин, соединённых ребром. Каждый раз когда мы добавляем ещё одно ребро, в конце его прибавляется так же и вершина. Следовательно, дерево с n вершинами имеет n-1 рёбер.
Дата добавления: 2015-10-05; просмотров: 1716;
