Эйлеровы графы и гамильтоновы циклы
Различают эйлеровы циклы и эйлеровы графы. Эйлеровым цикл можно считать следом пера, вычерчивающего этот цикл не отрываясь от бумаги.
Условия, при которых граф эйлеров.
Конечный неориентированный граф G эйлеров тогда и только тогда , когда он связан и степени всех его вершин четны.
В несвязном графе каждый цикл принадлежит какой-либо его связной части, т.е. не проходит через все его ребра.
В каждую вершину может входить несколько дуг при условии, что выходят они каждый раз по другим дугам. Т.о. их должно быть четное число.
Эйлеровы цепи. Так называется цепь, включающая все ребра данного конечного неориентированного графа G , но имеющая различное начало (U’) и конец (U”).
Чтобы в графе существовала эйлерова цепь, необходимы его связность и четность степеней всех вершин, кроме начальной и конечной. Последние две вершины должны иметь нечетные степени: из U’ мы лишний раз выходим, а в U” лишний раз входим. Эти условия достаточны для существования эйлеровой цепи.
Случай конечного ориентированного графа.
Чтобы в конечноориентированном графе существовал эйлеров цикл, необходимо и достаточно равенство степеней вершин графа по входящим и выходящим ребрам.
Т.к. любому неориентированному графу канонически соответствует ориентированный , в котором каждое ребро заменяется двумя направленными дугами, инцидентными тем же вершинам и идущими в противоположном направлении, то отсюда следует справедливость утверждения:
В конечном связном графе всегда можно построить ориентированный цикл, проходящий через каждое ребро по одному разу в каждом из двух направлений. Такой цикл иногда называется способом обхода всех дуг графа. Он используется во многих прикладных задачах, связанных с графами.
Гамильтоновым цикломназывается простой цикл, проходящий через все вершины рассматриваемого графа. Такой цикл существует не во всяком графе (рис.2.9).
 | |||
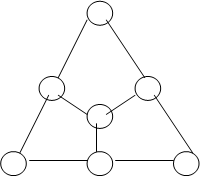 | |||
Да Нет
Рис.2.9 - Примеры графов
Несмотря на внешнюю схожесть, задачи распознавания эйлеровости и гамильтоновости графа принципиально различны. Правило определения эйлеровости приведено више. Что же касается гамильтоновости графа, то ответ на этот вопрос дает такая теорема, которая приводиться без доказательства: Граф со степенной последовательностью d1 £ d2 £ ... £ dn является гамильтоновым, если для всякого k, которое удовлетворяет неравенствам 1 £ k < n/2, истинна импликация (соответствие):
(dk £ k) Þ (dn-k ³ n - k) (2.8)
Существуют и другие, как более сильные, так і білее слабые теоремы и условия определения гамильтоновости графов.
Дата добавления: 2015-10-05; просмотров: 1237;
