Существуют следующие способы задания множеств.

1. Перечислением элементов множества. Например: А = {1, 3, 5, 7,9} - конечное множество; В = {1, 2,..., n,...} - бесконечное множество.

2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: А = {а| указание свойства элементов}. Здесь а является элементом множества A, а 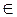А.

Пример 1.7.

Х= { х | х=2^к, где k= 1,2,3,...}.

А = {а | а — простое число}

В= {b|b²-1=0, b- действительное число}

Универсальным множеством называется такое множество U, что все рассматриваемые в данной задаче множества являются его подмножествами.

Для наглядного представления множеств и отношений между ними используются диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера - Венна).

Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, - в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.