Выбор начальных весов
Перед тем, как начинать процесс обучения нейронной сети, необходимо присвоить весам начальные значения. Цель здесь, очевидно, должна состоять в том, чтобы найти как можно более хорошее начальное приближение к решению и таким образом сэкономить время обучения и улучшить сходимость. Конечно, можно положить начальные веса во всей сети равными нулю, но тогда частные производные от невязки по всем весам будут одинаковыми, и изменения весов не будут должным образом структурированы. В результате нельзя будет надеяться на то, что сеть вообще когда-нибудь сможет решить задачу. Нужно искать способы уйти от такой симметрии.
Классический подход к выбору начальных значений весов состоит в следующем: случайным образом выбрать малые величины весов, чтобы быть уверенным, что ни один из сигмоидных элементов не насыщен (и значения всех производных очень малы). Например, если сигмовидный элемент имеет наибольшую производную в интервале [-3,3], подходящим выбором для начального веса будет случайное число, расположенное в интервале [ 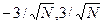 ], где N – число входов нейрона. Из-за малости величины начального веса последующие его изменения также будут небольшими, так как при этом учитывается абсолютная величина веса. Таким образом, нужно найти компромисс между существенными изменениями в значениях сигмоидов и малостью абсолютных величин.
], где N – число входов нейрона. Из-за малости величины начального веса последующие его изменения также будут небольшими, так как при этом учитывается абсолютная величина веса. Таким образом, нужно найти компромисс между существенными изменениями в значениях сигмоидов и малостью абсолютных величин.
Подобные правила рассчитаны на то, чтобы сеть начинала свою работу в линейном режиме и притом не на плоской части поверхности невязок. Однако нет гарантии, что такое начальное приближение приведет к глобальному минимуму или уменьшит время сходимости. Были разработаны другие методы, дающие еще более хорошее начальное приближение с точки зрения уменьшения времени обучения и обладающие большей устойчивостью в смысле локальных минимумов. При использовании обучающих алгоритмов типа ВР выбор начального приближения очень важен. Уже на этом шаге нужно позаботиться о том, чтобы не попасть в локальный минимум.
Дата добавления: 2015-09-18; просмотров: 934;
