Критерии ошибок
Целью процедуры минимизации является отыскание глобального минимума — достижение его называется сходимостью процесса обучения. Поскольку невязка зависит от весов нелинейно, получить решение в аналитической форме невозможно, и поиск глобального минимума осуществляется посредством итерационного процесса — так называемого обучающего алгоритма, который исследует поверхность невязки и стремится обнаружить на ней точку глобального минимума. Разработано уже более сотни разных обучающих алгоритмов, отличающихся друг от друга стратегией оптимизации и критерием ошибок.
Коль скоро обучение основывается на минимизации значения некоторой функции (показывающей, насколько результат, который выдает сеть на данном обучающем множестве, далек от образцового значения), нужно, прежде всего, выбрать меру ошибки, соответствующую сути задачи. Удачный выбор меры погрешности обычно приводит к более гладкой поверхности невязки и упрощает задачу обучения. Обычно в качестве меры погрешности берется средняя квадратичная ошибка, которая определяется как сумма квадратов разностей между желаемой величиной выхода dk и реально полученными на сети значениями уk для каждого примера k:
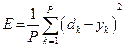 , (1.5)
, (1.5)
где Р— число примеров в обучающем множестве.
Наряду с такой мерой погрешности широко используется расстояние Кульбака-Лейблера, связанное с критерием максимума правдоподобия:
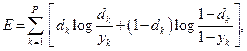 (1.6)
(1.6)
а также некоторые другие.
Для решения задач минимизации (1.5) (1.6) величины Е, существуют разнообразные методы. Например, вградиентном методеизменение весов W происходит в направлении, обратном к направлению наибольшей крутизны для функции E :
 , (1.7)
, (1.7)
где 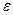 — определяемый пользователем параметр, который называется величиной шага или коэффициентом обучения;
— определяемый пользователем параметр, который называется величиной шага или коэффициентом обучения; 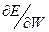 градиент функции E.
градиент функции E.
Другой возможный метод носит название стохастического градиентного. В нем веса пересчитываются после каждого просчета всех примеров из одного обучающего множества, и при этом используется частичная функция стоимости, соответствующая этому, например, k-му, множеству:
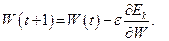
Дата добавления: 2015-09-18; просмотров: 832;
