Архитектура нейронных сетей

Для составление НС используется обычно несколько стандартных архитектур, из которых путем исключения лишнего или добавления строят большинство используемых сетей.

Очень важно согласовывать работу различных нейронов во времени. Как только в системе возникает более одного элемента, встает вопрос о синхронности их функционирования. Но для программных имитаторов нейронных сетей на цифровых ЭВМ такого вопроса нет в силу свойств основного компьютера, на котором реализуются нейронные сети. Для других способов реализации такой вопрос весьма важен. Здесь и далее будут рассматриваются только нейронные сети, синхронно функционирующие в дискретные моменты времени: все нейроны срабатывают «разом».

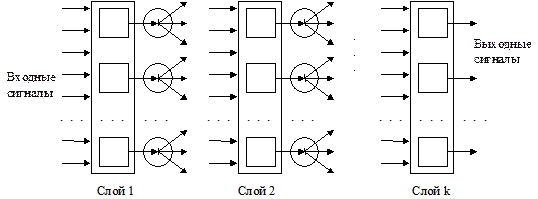Рис. 1.7. Слоистая сеть

В НС можно выделить две базовые архитектуры – слоистые и полносвязные сети.

Слоистые сети: нейроны расположены в несколько слоев (рис. 1.7). Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее срабатывает второй слой и т.д. до k-го слоя, который выдает выходные сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал i-го слоя подается на вход всех нейронов i+1-го. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал. Особое распространение получили трехслойные сети, в которых каждый слой имеет свое наименование: первый – входной, второй – скрытый, третий – выходной.

Полносвязные сети: каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам.

Элементы слоистых и полносвязных сетей могут выбираться по-разному. Существует, впрочем, стандартный выбор – нейрон с адаптивным неоднородным линейным сумматором на входе (рис. 1.5).

Для полносвязной сети входной сумматор нейрона фактически распадается на два: первый вычисляет линейную функцию от входных сигналов сети, второй – линейную функцию от выходных сигналов других нейронов, полученных на предыдущем шаге.

Функция активации нейронов (характеристическая функция) j – нелинейный преобразователь, преобразующий выходной сигнал сумматора (см. рис. 1.5) – может быть одной и той же для всех нейронов сети. В этом случае сеть называют однородной (гомогенной). Если же j зависит еще от одного или нескольких параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной).

Составление сети из нейронов стандартного вида (рис. 1.5) не является обязательным. Слоистая или полносвязная архитектуры не налагают существенных ограничений на участвующие в них элементы. Единственное жесткое требование, предъявляемое архитектурой к элементам сети, это соответствие размерности вектора входных сигналов элемента (она определяется архитектурой) числу его входов.

Если полносвязная сеть функционирует до получения ответа заданное число тактов k, то ее можно представить как частный случай k-слойной сети, все слои которой одинаковы и каждый из них соответствует такту функционирования полносвязной сети. Существенное различие между полносвязной и слоистой сетями возникает тогда, когда число тактов функционирования заранее не ограничено – слоистая сеть так работать не может.

Как говорилось ранее основу каждой НС составляют искусственные нейроны, то есть ячейка НС. Каждый нейрон характеризуется своим текущим состоянием. Текущее состояние нейрона определяется, как взвешенная сумма его входов:

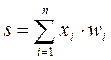, (1.1)

где w – весовой коэффициент входа нейрона.

Выход нейрона есть функция его состояния y = f(s).

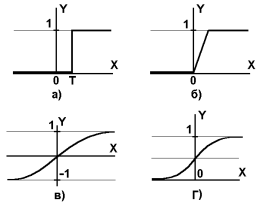Рис. 1.8. а) функция единичного скачка; б) линейный порог (гистерезис); в) сигмоид – гиперболический тангенс; г) сигмоид – формула (1.2)

Нелинейная функция f называется активационной и может иметь различный вид (рис. 1.8). Одной из наиболее распространеных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

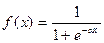. (1.2)

Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной

.

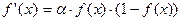Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям арг

ументов, где сигмоид имеет пологий наклон.

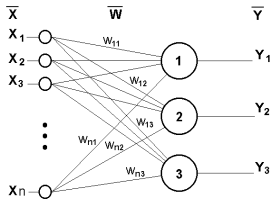Рис.1.9. Однослойный перцептрон

В качестве примера простейшей НС рассмотрим трехнейронный перцептрон (рис.1.9), то есть такую сеть, нейроны которой имеют активационную функцию в виде единичного скачка* . На n входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой НС и выдающие три выходных сигнала:

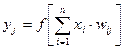, j=1,...,3. (1.3)

Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент w_ij задает величину i-ой синаптической связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме:

Y=F(XW),

где X и Y – соответственно входной и выходной сигнальные векторы, F( V) – активационная функция, применяемая поэлементно к компонентам вектора V.

Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется НС.

Очевидно, что процесс функционирования НС зависит от величин синаптических связей, поэтому, задавшись определенной структурой НС, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов.

Этот этап называется обучением НС. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.

Развивая дальше вопрос о возможной классификации НС, важно отметить существование бинарных и аналоговых сетей. Первые из них оперируют с двоичными сигналами, и выход каждого нейрона может принимать только два значения: логический ноль ("заторможенное" состояние) и логическая единица ("возбужденное" состояние). К этому классу сетей относится и перцептрон, так как выходы его нейронов, формируемые функцией единичного скачка, равны либо 0, либо 1. В аналоговых сетях выходные значения нейронов способны принимать непрерывные значения, что могло бы иметь место после замены активационной функции нейронов перцептрона на сигмоид.

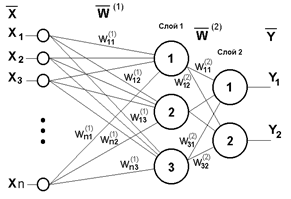Рис.1.10 Двухслойный перцептрон

Сети также можно классифицировать по числу слоев. На рис. 1.10 представлен двухслойный перцептрон, полученный из перцептрона (рис. 1.9) путем добавления второго слоя, состоящего из двух нейронов.

Какие задачи может решать НС? Грубо говоря, работа всех сетей сводится к классификации (обобщению) входных сигналов, принадлежащих n-мерному гиперпространству, по некоторому числу классов. С математической точки зрения это происходит путем разбиения гиперпространства гиперплоскостями (запись для случая однослойного перцептрона)

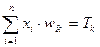, k=1,...,m. (1.4)

Каждая полученная область является областью определения отдельного класса. Число таких классов для одной НС перцептронного типа не превышает 2^m, где m – число выходов сети.

Функции, которые не реализуются однослойной сетью, называются линейно неразделимыми. Решение задач, подпадающих под это ограничение, заключается в применении 2-х и более слойных сетей или сетей с нелинейными синапсами, однако и тогда существует вероятность, что корректное разделение некоторых входных сигналов на классы невозможно.