Задания для тренинга. Фирма занимается реализацией подержанных автомобилей
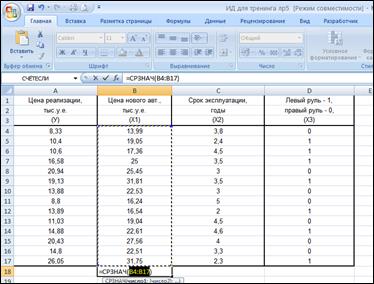
Фирма занимается реализацией подержанных автомобилей. Наименования показателей и исходные данные для эконометрического моделирования представлены в таблице (файл ИД для тренинга лр5.xls):
| Цена реализации, тыс.у.е. (У) | Цена нового авт., тыс.у.е. (Х1) | Срок эксплуатации, годы (Х2) | Левый руль - 1, правый руль - 0, (Х3) |
| 8,33 | 13,99 | 3,8 | |
| 10,40 | 19,05 | 2,4 | |
| 10,60 | 17,36 | 4,5 | |
| 16,58 | 25,00 | 3,5 | |
| 20,94 | 25,45 | 3,0 | |
| 19,13 | 31,81 | 3,5 | |
| 13,88 | 22,53 | 3,0 | |
| 8,80 | 16,24 | 5,0 | |
| 13,89 | 16,54 | 2,0 | |
| 11,03 | 19,04 | 4,5 | |
| 14,88 | 22,61 | 4,6 | |
| 20,43 | 27,56 | 4,0 | |
| 14,80 | 22,51 | 3,3 | |
| 26,05 | 31,75 | 2,3 |
Требуется:
1. Рассчитать матрицу парных коэффициентов корреляции; определить наиболее информативный фактор.
Используем MS Excel / Данные / Анализ данных / КОРРЕЛЯЦИЯ:
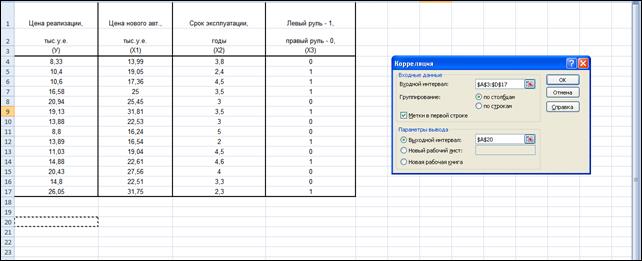
Входной интервал – это вся таблица данных вместе с заголовками. Так как, заголовки были выбраны, то поставьте √ в поле Метки. Задайте выходной интервал.
Получим матрицу коэффициентов парной корреляции между всеми имеющимися переменными:
| У | Х1 | Х2 | Х3 | |
| У | ||||
| Х1 | 0,910987 | |||
| Х2 | -0,4156 | -0,2603 | ||
| Х3 | 0,190785 | 0,221927 | -0,30308 |
Проанализируем коэффициенты корреляции между результирующим признаком Y и каждым из факторов Xj:
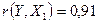> 0, следовательно, между переменными Y и Х1 наблюдается прямая корреляционная зависимость: чем выше цена нового автомобиля, тем выше цена реализации.
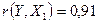> 0,7 – эта зависимость является тесной.
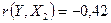< 0, значит, между переменными Y и Х2 наблюдается обратная корреляционная зависимость: цена реализации ниже для автомобилей с большим сроком эксплуатации.
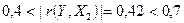– эта зависимость умеренная, ближе к слабой.
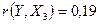> 0, значит, между переменными Y и Х3 наблюдается прямая корреляционная зависимость: цена реализации выше для автомобилей с левым рулем.
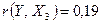< 0,4 – эта зависимость слабая.
Таким образом, наиболее тесная и значимая зависимость наблюдается между ценой реализации Y и ценой нового автомобиля Х1.
2. Построить регрессионную модель от наиболее информативного фактора.
Для построения парной линейной модели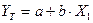 
используем программу РЕГРЕССИЯ (Данные/ Анализ данных). В качестве «входного интервала Х» покажем значения фактора Х1.
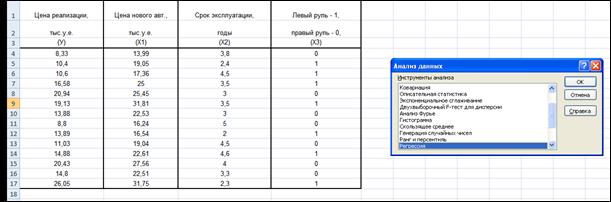
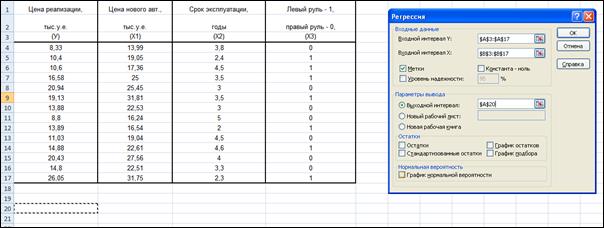
Результаты вычислений представлены в таблицах:
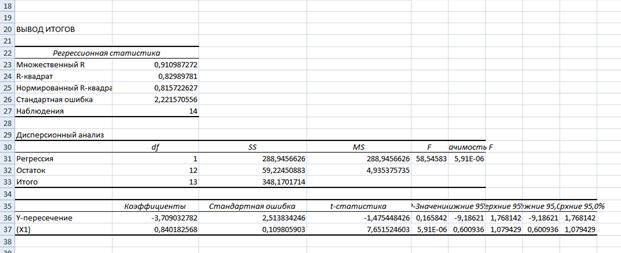
Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ (столбец Коэффициенты).
Таким образом, модель (1) построена, ее уравнение имеет вид
.
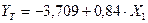Коэффициент регрессии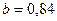 
, следовательно, при увеличении цены нового автомобиля (Х1) на 1 тыс.у.е. цена реализации (У) увеличивается в среднем на 0,84 тыс.у.е.
Свободный член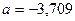 
в данном уравнении не имеет реального смысла.
3. С использованием модели осуществить прогнозирование среднего значения показателя У, если прогнозное значение фактора Х1 увеличится на 20% от его среднего значения.
Согласно условию задачи прогнозное значение факторной переменной Х1 составит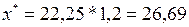 
.
Рассчитаем по полученному уравнению модели прогнозное значение показателя У:
.
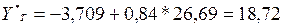Таким образом, если цена нового автомобиля увеличится на 20% от среднего значения и составит 26,69 тыс.у.е., то ожидаемая цена реализации будет около 18,72 тыс.у.е.
Дата добавления: 2015-09-18; просмотров: 1263;