Регрессия и задача прогнозирования
Для построения уравнения регрессии необходимо определить факторы, от которых планируется построить уравнение.
Информативность факторов можно оценить с использованием коэффициента парной корреляции.
Показателем тесноты линейной взаимосвязи между переменными Х и Y является выборочный коэффициент парной корреляции 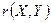 .
.
Величину коэффициента корреляции можно найти в MS Excel с помощью: Данные/ анализ данных / КОРРЕЛЯЦИЯ
1. если r > 0, то говорят о прямой корреляционной зависимости между Х и Y: при увеличении Х величина Y имеет тенденцию в среднем возрастать;
2. если r < 0, то говорят об обратной корреляционной зависимости между Х и Y: при увеличении Х величина Y имеет тенденцию в среднем уменьшаться;
3. в зависимости от того, насколько 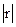 приближается к 1, различают три уровня корреляционной зависимости:
приближается к 1, различают три уровня корреляционной зависимости:
- слабую (при 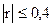 ),
),
- умеренную (при 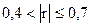 ),
),
- тесную (при 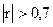 ).
).
Практически в каждом отдельном случае результирующая величина Y складывается из двух слагаемых:
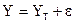 ,
,
где Y – фактическое значение результирующего показателя;
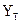 – теоретическое (расчетное) значение этого показателя;
– теоретическое (расчетное) значение этого показателя;
e – случайная величина, характеризующая отклонение фактического значения Y от расчетного 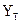 из-за неучтенных в модели факторов и случайных ошибок.
из-за неучтенных в модели факторов и случайных ошибок.
Уравнение 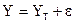 называется уравнением регрессии.
называется уравнением регрессии.
Построить модель – значит определить ее коэффициенты и записать ее уравнение не в общем, а в пригодном для расчетов виде.
Универсальным способом построения линейных моделей (как парных, так и множественных) является в MS Excel программа РЕГРЕССИЯ (Данные / анализ данных / РЕГРЕССИЯ).
Прогнозирование – это оценка значений результирующего показателя Y в некоторой, представляющей практический интерес прогнозной ситуации, которая описывается факторными переменными Х*.
Прогнозные значения Х* факторных переменных либо задаются, либо рассчитываются отдельно. Предполагают, что в период прогнозирования сохраняются существующие взаимосвязи между переменными.
Точечный прогноз величины Y выполняется по уравнению модели путем подстановки в него соответствующих значений факторных переменных 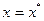 .
.
В случае парной модели 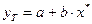 - ожидаемое значение признака Y.
- ожидаемое значение признака Y.
Реальные значения Y скорее всего будут отличаться от рассчитанных прогнозных 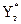 . Это отличие объясняется двумя причинами:
. Это отличие объясняется двумя причинами:
1) расчет 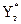 проведен по уравнению регрессии, коэффициенты aj которого найдены по выборочным данным, являются случайными величинами со стандартными отклонениями S(aj). Значит
проведен по уравнению регрессии, коэффициенты aj которого найдены по выборочным данным, являются случайными величинами со стандартными отклонениями S(aj). Значит 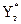 – тоже случайная величина и имеет стандартное отклонение
– тоже случайная величина и имеет стандартное отклонение 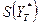 ;
;
2) согласно уравнению эконометрической модели 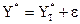 , т.е. реальное (индивидуальное) значение результирующего признака может отклоняться от расчетного (теоретического) на случайную величину e, что увеличивает стандартную ошибку
, т.е. реальное (индивидуальное) значение результирующего признака может отклоняться от расчетного (теоретического) на случайную величину e, что увеличивает стандартную ошибку 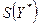 по сравнению с
по сравнению с 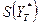 .
.
Дата добавления: 2015-09-18; просмотров: 1018;
