Задания для отчета по лабораторной работе. 1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см

1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см. Определить момент инерции 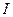системы относительно оси, перпендикулярной стержню и проходящей через центр масс.

2. Два шара массами m и 2m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рис. 4. Определить момент инерции 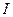системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.

3. Два шара массами 2m и m (m = 20 г) закреплены на тонком невесомом стержне длиной l = 1 м так, как это показано на рис. 5 Определить момент инерции 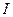системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.

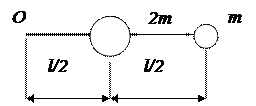
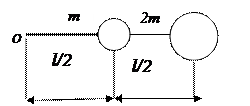
Рис. 4 (к задаче 2) Рис. 5 (к задаче 3)

4. Определить момент инерции трехатомной молекулы H₂O (рис. 6) относительно оси y, проходящей через центр масс молекулы. Межъядерное расстояние AB обозначено d = 0,097 нм, α = 104^о30' .

5. Определить момент инерции трехатомной молекулы SO₂ (рис. 6) относительно оси x, проходящей через центр масс молекулы

(d = 0, 145 нм, α = 124^о).

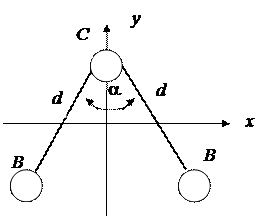
Рис. 6 (к задаче 6)

6. Определить момент инерции тонкого однородного стержня длиной l = 30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины. Определить момент инерции 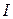тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на

a = 20 см от одного из его концов.

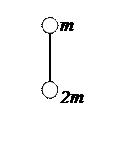7. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции 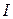такой системы относительно оси, перпендикулярной стержню и проходящей через точку, лежащую на середине стержня (рис. 7).

Рис. 7 (к задаче 7)

8. Вычислить момент инерции J проволочного прямоугольника со сторонами a = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью 0,1 кг/м.

9. Определить момент инерции 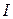проволочного равностороннего треугольника со стороной a = 10 см относительно: оси, лежащей в плоскости треугольника и проходящей через его вершину и середину противоположной стороны.

10. Определить момент инерции 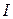кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной кольцу.

11. Диаметр диска d = 20 см, масса m = 800 г. Определить момент инерции 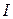диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.

12. Найти момент инерции 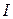плоской однородной прямоугольной пластины массой m = 800 г относительно оси, совпадающей с одной из ее сторон, если длина a другой стороны равна 40 см.

13. Определить момент инерции 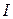тонкой плоской пластины со сторонами a = 10 см и b =20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью 1,2 кг/м².

14. В однородном диске массой m = 1 кг и радиусом R = 30 см вырезано круглое отверстие диаметром d =20 см, центр которого находится на расстоянии l = 15 см от оси диска (рис. 8). Найти момент инерции 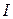полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.

15. На однородный сплошной цилиндр массой M и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массой m (рис .9). В момент времени t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени модуля угловой скорости цилиндра.

Рис. 8 (к задаче 14) Рис. 9 ( к задаче 15)

16. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m₁ = 0,3 кг и m₂ = 0,5 кг. Определить силы T₁и T₂ натяжения нити по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

17. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m₁ = 100 г и m₂ = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г. Трение при вращении блока ничтожно мало.

18. Два тела массами m₁ = 0,25 г и m₂ = 0,15 г связаны тонкой нитью, переброшенной через блок (рис. 10). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m₁.

С каким ускорением движутся тела, и каковы силы T₁ и T₂ натяжения нити по обе стороны блока? Коэффициент трения µ тела о поверхность стола равен 0,2. Масса m блока равна 0,1 г, и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.

19. Однородный сплошной цилиндр массой m = 1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис.11). Цилиндр отпускают без толчка. а) За сколько времени t цилиндр опустится на расстояние y =50 см? б) Какое натяжение F испытывает при опускании цилиндра каждая из нитей?

Рис. 10 ( к задаче 18) Рис. 11 ( к задаче 19)