Принцип устройства и расчета шкал счетной линейки

Навигационная счетная линейка НЛ-10 построена по типу логарифмических линеек.

Как известно, основные свойства логарифмов заключаются в следующем:

1) Логарифм произведения двух чисел равен сумме логарифмов чисел

Lg a b=lg a+lg b

2) Логарифм частного двух чисел равен разности логарифмов делимого и делителя

lg 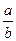= lg a — lg b.

3) Логарифм степени равен логарифму основания, умноженному на показатель степени

lg a² = 2 lg a (квадрат числа);

lg 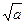= 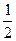lg а (корень квадратный из числа).

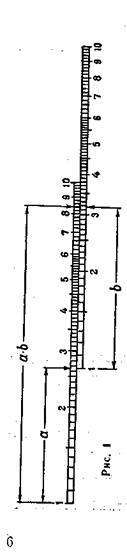Эти свойства позволяют более сложные математические действия с числами — умножение и деление, извлечение корня и возведение в квадрат — заменить простыми действиями с их логарифмами — сложением и вычитанием отрезков шкал, на которых нанесены в определенном масштабе значения логарифмов чисел (рис. 1).

Кроме того, у десятичных логарифмов (логарифмы, основанием которых является число 10) мантиссы логарифмов чисел N, 10N, 100N и т.д. равны между собой. Это позволяет на всю длину линейки нанести шкалу с одним или двумя — тремя разными интервалами от О до 1 (от lg 1 до lg 10), оцифровать их (от 1 до 10 — первый интервал, от 10 до 100 — второй и от 100 до 1000 — третий) и пользоваться ими для любых чисел, величина которых кратна 10, Так, деление 60 шкалы I(см. рис.3) можно считать равным 0,6; 6; 600 и т. д.

При наличии нескольких интервалов (периодов) упрощается установка исходных величин и .отсчет результатов (одним перемещением движка), но при этом деления шкалы становятся мельче и точность отсчета снижается. Поэтому, если вычисления не связаны с решением специальных задач (пересчет приборной высоты, скорости и т д.), лучше пользоваться шкалой с наиболее крупным масштабом (шкалы 14 и 15).

Обычно за начало логарифмической шкалы берут 1, так как lg 1 = 0, а величина интервала (масштаб или модуль шкалы) выбирается в зависимости от размеров линейки и заданной точности вычислений. Например, на линейке НЛ-10 по всей длине нанесены три интервала от 1 до 10 (шкалы 1, 2, 5) с модулем М = 84 мм, полтора интервала (шкала 6) и даже части интервалов. Обычно эти шкалы имеют размерные величины и служат для специальных целей.

В таких случаях начало шкалы вынесено за пределы размеров линейки в так называемый условный «нуль» Его положение зависит от расположения шкал линейки или от того, какой участок шкалы необходимо использовать.

Следует иметь в виду, что участки логарифмических шкал имеют неравные деления. Например, деление от 1 до 2 (от 10 до 20) неравноценно делению от 8 до 9 или от 9 до 10. Это объясняется свойством логарифмической функции, которая изменяется неравномерно с изменением величины от 1 до 10 (от 10 до 100 и т д.).