Резонанс. Резонанс – резкое возрастание амплитуды вынужденных колебаний осциллятора: А =max

Резонанс – резкое возрастание амплитуды вынужденных колебаний осциллятора: А =max. Это возможно, когда ω ≈ω₀.

Знаменатель должен быть минимальным:

(ω₀² – ω²)² + 4 β² ω² = min,

т.е. производная должна быть равна 0. Взяв производную по ω, получаем: .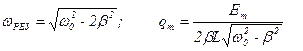

Если β = 0 (нет R), то ω_рез = ω₀ и q_m = ∞. Когда ω = 0, то q_m = E_m • С

На рисунках представлены резонансные кривые для q_m и I_m. Резонансные кривые для U_Cm такие же как и для q_m.

.

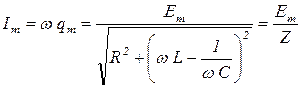Когда ω = 0, то I_m = 0;

I_m = max, если

.

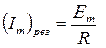
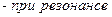Форма резонансных кривых связана с добротностью контура Q. Добротность контура связана с шириной резонансной кривой: Δω – ширина резонансной кривой. Δω находится на «высоте», равной 0,7 от максимальной, т.е. в резонансе.

Следовательно, острота резонансной кривой связана с добротностью контура.

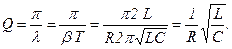
Из векторной диаграммы: ,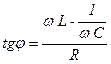

φ – сдвиг по фазе между током I и E.

При резонансе I_m = max и т.е.сила тока I и приложенное напряжение E изменяются синфазно. Тогда Z = min → Z = R →

U_R = E = U, т.е. внешнему напряжению, и U_mC = U_mL, но противоположны по фазе.

Такой резонанс (последовательный резонанс) называется резонансом напряжений.

.

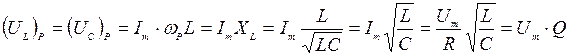Так как. Q > 1,то U_L > U и U_С > U, поэтому резонанс напряжений используется в технике для усиления колебаний напряжения какой-либо определенной частоты.

Резонанс напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, т.к. иначе может наблюдаться пробой.