Затухающие колебания
Реальный контур обладает активным сопротивлением R. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают.
По закону Ома имеем:

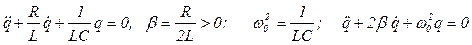 –
–
дифференциальное уравнение затухающих колебаний. Решение этого уравнения:
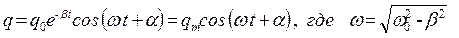 – частота затухающих колебаний; β – коэффициент затухания, qm = A – амплитуда затухающих колебаний, убывающая со временем по экспоненциальному закону:
– частота затухающих колебаний; β – коэффициент затухания, qm = A – амплитуда затухающих колебаний, убывающая со временем по экспоненциальному закону:
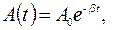
где А0 – начальная амплитуда. Таким образом, амплитуда затухающих колебаний уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания β.
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний пользуются понятием логарифмического декремента затухания.
Логарифмическим декрементом затухания называется безразмерная величина λ, равная натуральному логарифму отношения значений амплитуды затухающих колебаний в моменты времени t и t+T (Т – период колебаний):
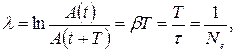
где τ – время релаксации, Ne – число колебаний, совершаемых за время релаксации τ.
Промежуток времени τ, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации:
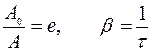 .
.
Для характеристики затухания часто пользуются и другой величиной, называемой добротностью контура Q.
Добротность Q связана с λ соотношением: 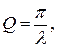 т.к.
т.к. 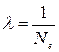 , то
, то 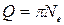 .
.
Таким образом, добротность контура Q – есть умножение на π числа полных колебаний, по истечении которых амплитуда уменьшается в е раз. Следовательно, Q контура тем выше, чем меньше затухание колебаний в контуре.
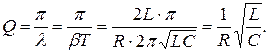
Дата добавления: 2015-09-18; просмотров: 688;
