Математичний маятник

Математичний маятник¾ точкове тіло маси m, підвішене на нерозтяжному підвісі L (див.Мал.32), розмірами якого, порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m і нею також можна знехтувати. Коливання описуються кутом відхилення тіла від положення рівноваги ¾ 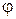, кутовою швидкістю 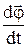та кутовим прискоренням 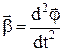. Вектор 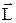задає точку прикладання сил. 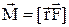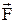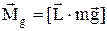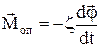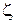Коливання здійснюються в загальному випадку під дією моменту зовнішніх сил , моменту сили тяжіння та моменту сил опору , де ¾ коефіцієнт опору. Вектори моментів сил 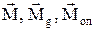та кутового прискорення 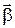лежать на осі обертання, яка ^ площині коливання та проходить через центр обертання О.

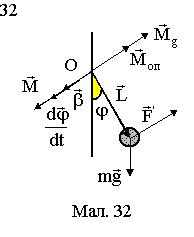Величину моменту сили тяжіння можна записати у вигляді 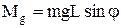. Для малих кутів j маємо sinj­ » j і 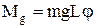. Такі коливання називаються малими. За другим законом Ньютона для обертового руху маятникарівняння коливань можна записати так

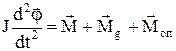, (1)

де J=mL² ¾ момент інерції точкового тіла. Вектори 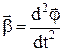, , 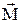, 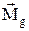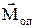лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння (1) можна записати в алгебраїчній формі

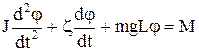. (2)

В канонічному вигляді це рівняннямає вигляд:

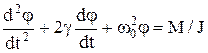, (3)

де 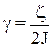¾ коефіцієнт згасання коливань, 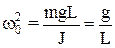, w₀ ¾ частота вільних незгасаючих коливань, або частота власнихколивань маятника.

4.4. Фізичний маятник

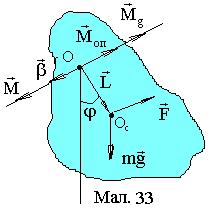
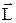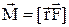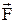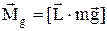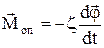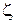Фізичний маятник¾ макроскопічне тіло, що здійснює малі коливання. Вісь обертання маятника О зміщена відносно центра мас тіла O_c на вектор (див.Мал.33). Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту зовнішніх сил , моменту сили тяжіння та моменту сил опору , де ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: М_g = mgLsinj. Для малих коливань маятника маємо sinj­ » j і М_g = mgLj.

Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:

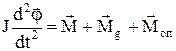, (1)

де J ¾ момент інерції тіла. Вектори 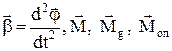лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:

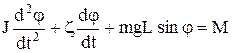. (2)

В канонічному вигляді рівняння(2) можна записати так

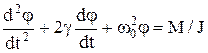, (3)

де 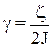¾ коефіцієнт згасання коливань, 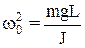, w₀ ¾ частотавільних незгасаючих коливань. Період малих власних коливань маятникаT₀ = 2p/w₀ і T₀ = 2p 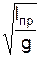, де 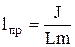¾ приведена довжина фізичного маятника, яка є довжиною підвісу математичного маятника з періодом рівним періоду коливань фізичного маятника.