РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
Воспользуемся полученной нами ранее барометрической формулой:
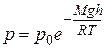 (9.16)
(9.16)
и получим зависимость концентрации молекул от высоты. Поскольку
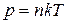 ,
,  и
и 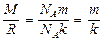 , то
, то
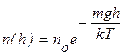 (9.17)
(9.17)
 Если изобразить графики зависимостей
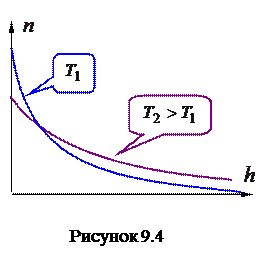
Если изобразить графики зависимостей 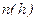 в соответствии с (9.17) при различных температурах, то легко видеть, что с понижением температуры основная часть молекул располагается ближе к поверхности Земли. При абсолютном нуле все молекулы должны были бы расположиться на поверхности. Наоборот, при высоких температурах молекулы располагаются почти равномерно.
в соответствии с (9.17) при различных температурах, то легко видеть, что с понижением температуры основная часть молекул располагается ближе к поверхности Земли. При абсолютном нуле все молекулы должны были бы расположиться на поверхности. Наоборот, при высоких температурах молекулы располагаются почти равномерно.
Конкретное распределение молекул устанавливается в результате действия противоположных факторов: сила притяжения концентрирует молекулы вблизи поверхности, а тепловое движение разбрасывает по всем высотам.
В числителе показателя степени экспоненты (9.17) стоит фактически энергия молекулы в поле силы тяжестиεр. Поэтому (9.17) можно записать в виде
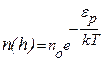 (9.18)
(9.18)
Больцман доказал, что распределение (9.18) справедливо для совокупности любых одинаковых частиц, находящихся в тепловом движении в любом потенциальном поле. Поэтому распределение (18) называют распределением Больцмана. Это распределение можно представить в виде
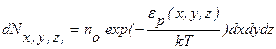 (9.19)
(9.19)
где 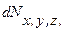 – количество молекул, попадающих в пределы объема
– количество молекул, попадающих в пределы объема 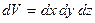 , расположенного в точке с координатами x, y, z.
, расположенного в точке с координатами x, y, z.
Это распределение можно объединить с распределением Максвелла, выделив из 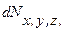 молекулы, компоненты скорости которых лежат в пределах от
молекулы, компоненты скорости которых лежат в пределах от 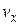 до
до 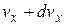 ,от
,от 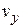 до
до 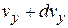 , от
, от 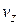 до
до 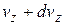 :
:
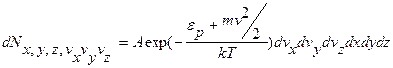 (9.20)
(9.20)
Очень часто энергия частиц может только дискретные значения из ряда: 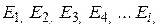 . В этом случае распределение Больцмана дает количество частиц
. В этом случае распределение Больцмана дает количество частиц 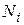 , которые находятся в состоянии с энергией
, которые находятся в состоянии с энергией 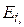 и имеет вид:
и имеет вид:
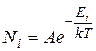 (9.21)
(9.21)
где 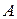 – коэффициент пропорциональности, который определяется из условия нормировки. В этом случае условие нормировки сводится к требованию того, чтобы сумма частиц во всех состояниях была равна общему количеству частиц в системе:
– коэффициент пропорциональности, который определяется из условия нормировки. В этом случае условие нормировки сводится к требованию того, чтобы сумма частиц во всех состояниях была равна общему количеству частиц в системе:
 (9.22)
(9.22)
Найдем значение нолрмирующего множителя, подставив (9.21) в (9.22):
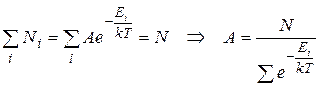 (9.23)
(9.23)
Таким образом, окончательно распределение Больцмана для систем с дискретными разрешенными значениями энергии можно записать в виде:
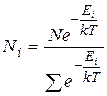 (9.24)
(9.24)
Дата добавления: 2015-09-14; просмотров: 814;
