ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ТЕПЛОЕМКОСТИ
Согласно рассмотренной нами классической теории теплоемкости у газов она должна быть кратной 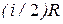 и не зависеть от температуры. На рисунке 8.4 показан примерный вид температурной зависимости теплоемкости водорода, полученной экспериментально. Имеются три температурных интервала (
и не зависеть от температуры. На рисунке 8.4 показан примерный вид температурной зависимости теплоемкости водорода, полученной экспериментально. Имеются три температурных интервала (  ,
,  ,
,  ), на которых поведение приблизительно соответствует классической теории. Но число степеней свободы, молекул проявляющееся в теплоемкости, в каждом интервале различно. При промежуточных значениях температуры теплоемкость такова, что молекулы как бы имеют дробное количество степеней свободы.
), на которых поведение приблизительно соответствует классической теории. Но число степеней свободы, молекул проявляющееся в теплоемкости, в каждом интервале различно. При промежуточных значениях температуры теплоемкость такова, что молекулы как бы имеют дробное количество степеней свободы.
 В соответствии со значением теплоемкости можно говорить, что при низких температурах молекулы участвуют только в поступательном движении – интервал
В соответствии со значением теплоемкости можно говорить, что при низких температурах молекулы участвуют только в поступательном движении – интервал  , в интервале
, в интервале  – в поступательном и вращательном, а при температурах, соответствующих интервалу
– в поступательном и вращательном, а при температурах, соответствующих интервалу  включается еще и колебательная степень свободы: связь между атомами перестает быть жесткой.
включается еще и колебательная степень свободы: связь между атомами перестает быть жесткой.
В интервалах температуры, соответствующие переходу от одного участка к другому, температурный ход теплоемкости может быть объяснен тем, что не все молекулы одновременно начинают участвовать в новом виде движения, и доля таких молекул увеличивается с ростом температуры.
 Объяснение такого поведения молекул может быть дано только квантовой механикой. Согласно квантовомеханическим представле-ниям энергия вращательного и колебательного движений может измениться только порциями определенной величины, т.е. квантуется. Промежуточных значений энергии у молекулы быть не может. Кроме того, порции энергии (кванты), а значит и расстояния между разрешенными значениями энергии для колебательного движения приблизительно на порядок больше, чем для вращательного движения (рисунок 8.5).
Объяснение такого поведения молекул может быть дано только квантовой механикой. Согласно квантовомеханическим представле-ниям энергия вращательного и колебательного движений может измениться только порциями определенной величины, т.е. квантуется. Промежуточных значений энергии у молекулы быть не может. Кроме того, порции энергии (кванты), а значит и расстояния между разрешенными значениями энергии для колебательного движения приблизительно на порядок больше, чем для вращательного движения (рисунок 8.5).
Энергии молекул, как и скорости, группируются вблизи некоторого наиболее вероятного значения. Подавляющая часть молекул имеет приданной температуре энергии не очень сильно отличающиеся от наиболее вероятного значения.
Эти особенности энергетического спектра молекул приводят к тому, что при низких температурах, когда вероятное значение энергии намного меньше порции (кванта) энергии, необходимой для вовлечения молекулы во вращательное движение, в подавляющем большинстве молекулы будут участвовать только в поступательном движении. В интервале температур, когда наиболее вероятная энергия приблизительно равна кванту энергии вращательного движения, с ростом температуры все большая часть молекул начинает участвовать во вращательном движении. Соответственно теплоемкость в этом интервале быстро изменяется от 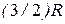 до
до 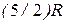 . При дальнейшем росте температуры характер движения молекул не изменяется до тех пор, пока вероятная энергия молекул не начнет приближаться к величине кванта колебательного движения. Достижение основной массой молекул энергий, соответствующих кванту колебательного движения, означает вовлечение большинства молекул в колебательное движение. Этому процессу соответствует второй участок быстрого роста теплоемкости.
. При дальнейшем росте температуры характер движения молекул не изменяется до тех пор, пока вероятная энергия молекул не начнет приближаться к величине кванта колебательного движения. Достижение основной массой молекул энергий, соответствующих кванту колебательного движения, означает вовлечение большинства молекул в колебательное движение. Этому процессу соответствует второй участок быстрого роста теплоемкости.
 8.4. ПОНЯТИЕ О ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
8.4. ПОНЯТИЕ О ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
Рассмотрим некоторую макроскопическую систему, и пусть какая-то характерная для системы величина 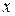 может принимать дискретные значения:
может принимать дискретные значения:
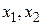

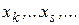
Проведем большое количество измерений  величины
величины 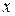 , так чтобы при каждом измерении система находилась бы в одном и том же определенном состоянии. Допустим, что результат
, так чтобы при каждом измерении система находилась бы в одном и том же определенном состоянии. Допустим, что результат 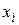 появился в
появился в  измерениях. Тогда, по определению отношение
измерениях. Тогда, по определению отношение 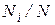 называется относительной частотой появления результата
называется относительной частотой появления результата 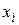 , а предел этого отношения при неограниченном возрастании
, а предел этого отношения при неограниченном возрастании 
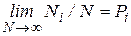 . (8.14)
. (8.14)
называется вероятностью появления результата 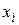 .
.
Отметим, что поскольку
 то
то 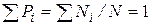
Зная вероятности появления различных результатов, можно найти среднее значение измеряемой величины:
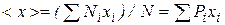 . (8.15)
. (8.15)
 Допустим теперь, что величина
Допустим теперь, что величина 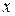 может принимать непрерывный ряд значений, т.е. имеет непрерывный спектр значений. Значения измеряемой величины будем откладывать вдоль некоторой оси. Разобьем ось значений
может принимать непрерывный ряд значений, т.е. имеет непрерывный спектр значений. Значения измеряемой величины будем откладывать вдоль некоторой оси. Разобьем ось значений 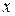 на очень маленькие интервалы
на очень маленькие интервалы 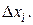 Пусть в результате проведения очень большого числа измерений
Пусть в результате проведения очень большого числа измерений  в
в 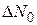 измерениях результат оказался в пределах от
измерениях результат оказался в пределах от 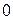 до
до 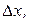 в
в 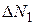 измерениях – от
измерениях – от 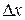 до
до 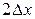 , и т. д. в
, и т. д. в 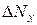 измерениях результат оказался в интервале от
измерениях результат оказался в интервале от 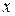 до
до 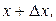 и т.д. Если измерений количество
и т.д. Если измерений количество  достаточно велико, то вероятность того, что при измерении результат окажется в пределах от
достаточно велико, то вероятность того, что при измерении результат окажется в пределах от 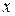 до
до 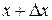
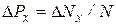 . (8.16)
. (8.16)
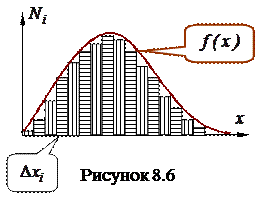
Для наглядного изображения распределения вероятности получения результата в интервале от 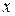 до
до 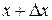 , построим столбики шириной
, построим столбики шириной 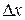 и высотой
и высотой 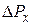 перпендикулярно оси
перпендикулярно оси 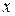 . Полученная в результате такого построения диаграмма называется гистограммой.
. Полученная в результате такого построения диаграмма называется гистограммой.
При  ступенчатая линия, ограничивающая гистограмму сверху стремится к кривой. Функция,
ступенчатая линия, ограничивающая гистограмму сверху стремится к кривой. Функция, 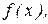 определяющая эту кривую, называется функцией распределения вероятностей. Действительно, площадь столбика шириной
определяющая эту кривую, называется функцией распределения вероятностей. Действительно, площадь столбика шириной  , ограниченного сверху графиком
, ограниченного сверху графиком 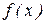 дает вероятность
дает вероятность 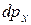 получения в результате изменения значения
получения в результате изменения значения 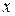 в интервале от
в интервале от 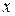 до
до 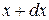 :
:
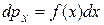 . (8.17)
. (8.17)
Площадь, ограниченная всей кривой 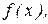 дает вероятность получения какого-либо значения
дает вероятность получения какого-либо значения 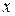 . Поскольку какое-нибудь значение в результате измерения получается, эта вероятность равна единице:
. Поскольку какое-нибудь значение в результате измерения получается, эта вероятность равна единице:
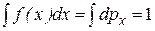 . (8.18)
. (8.18)
Знание 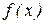 позволяет находить среднее значение измеряемой величины
позволяет находить среднее значение измеряемой величины 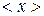 . Действительно, результат, лежащий в окрестности
. Действительно, результат, лежащий в окрестности 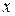 получается в
получается в 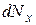 измерениях. По аналогии с соотношением (8.15)
измерениях. По аналогии с соотношением (8.15) 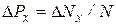
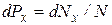 . (8.19)
. (8.19)
Приравнивая правые части (8.17) и (8.19), получаем:
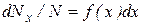 . (8.20)
. (8.20)
и находим:
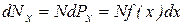 . (8.21)
. (8.21)
Сумму результатов измерений для тех случаев, когда 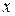 оказался в интервале от
оказался в интервале от 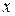 до
до 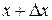 , дает произведение
, дает произведение 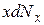 :
:
 . (8.22)
. (8.22)
Тогда сумма всех возможных результатов измерений будет равна
 . (8.23)
. (8.23)
Разделив эту сумму на общее число измерений  , получим среднее значение
, получим среднее значение 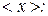
 . (8.24)
. (8.24)
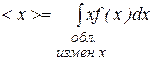 . (8.24)
. (8.24)
Рассуждая аналогичным образом, приходим к выводу, что среднее значение произвольной функции от 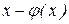 - находится по формуле
- находится по формуле
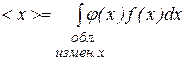 . (8.25)
. (8.25)
Дата добавления: 2015-09-14; просмотров: 2040;
