Теорема Шеннона для непрерывных каналов с помехами

Производительность источника непрерывных сообщений пропорциональна энтропии источника 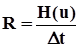. Поскольку энтропия источника непрерывных сигналов – бесконечно большая, то и производительность такого источника – бесконечно большая. На практике даже при безошибочной передаче сигнала по каналу связи приемник воспринимает поступивший сигнал с какой-то погрешностью.

Принятое сообщение Z(t) и переданное X(t) называются эквивалентными, если различие между ними несущественно в смысле выбранного критерия (обычно это критерий среднеквадратичного отклонения). Вводится понятие отклонения ε(t) = x(t) – z(t), задается предельная погрешность 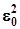. Если среднее за период отклонение < 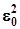, то реализации считаются эквивалентными.

Эпсилон-энтропией H_ε(X) называется минимальное среднее количество информации, содержащееся в одном отсчете сообщения Z(t) относительно сообщения X(t), при котором эти сообщения еще эквивалентны.

В соответствии с соотношением H_ε(X) = min {I(X,Z) | 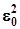≥ε²}эпсилон-энтропия определяет количество существенной информации, содержащейся в одном отсчете непрерывного сообщения.

Производительность источника определяется как 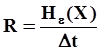. По теореме Котельникова , где F –полоса пропускания, значит R = 2F∙H_ε(X).

Теорема Шеннона для непрерывного канала с помехами (третья теорема):

Если при заданном критерии эквивалентности сообщений 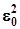произво­ди­тельность источника информации меньше пропускной способности канала, то есть R < C, то существует такой способ кодирования и декодирования в обобщенном смысле (т. е. преобразование сообщения в сигнал и обратно), при котором неточность воспроизведения сообщения сколь угодно близка к 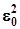. При R > C такого способа не существует.

Глава 6
Помехоустойчивое кодирование сообщений

Мы рассмотрели основы эффективного кодирования данных, задача которого – представить подлежащие передаче данные в максимально компактной и, по возможности, неискаженной форме.

При передаче информации по каналу связи с помехами в принятых данных могут возникать ошибки. Если такие ошибки имеют небольшую величину или возникают достаточно редко, информация может быть использована потребителем. При большом числе ошибок полученной информацией пользоваться нельзя.

Ранее уже говорилось о понятии помехоустойчивости (способности информационных систем противостоять воздействию помех). Для реализации принципа помехоустойчивости информационных систем может быть использовано помехоустойчивое кодирование.

Помехоустойчивыми (корректирующими) называются коды, позволяющие обнаружить и при необходимости исправить ошибки в принятом сообщении.

Возможность использования кодирования для уменьшения числа ошибок в канале была теоретически показана К. Шенноном в 1948 году в его работе "Математическая теория связи". Теперь это утверждение принято именовать второй теоремой Шеннона.