Систематические коды

Систематические коды относятся к группе блочных разделимых кодов. Для систематического кода сумма по модулю 2 двух разрешенных комбинаций также дает разрешенную комбинацию (свойство замкнутости). Все разрешенные комбинации систематического (n, k)-кода можно получить, располагая k-значными исходными комбинациями. При этом:

v в число исходных комбинаций не должна входить тривиальная (нулевая);

v все исходные комбинации должны быть линейно независимы, т.е. ни одна из них не может быть получена путем суммирования других;

v для обеспечения требуемой корректирующей способности минимальное кодовое расстояние d_min исходных комбинаций должно удовлетворять условиям Хемминга.

Получение кодовых комбинаций производится с помощью порождающих матриц, состоящих из k строк и n столбцов:

В классической (канонической) форме кода элементы первых k столбцов служат для информационных целей, а оставшихся – для проверочных. Соответственно, порождающую матрицу G можно представить в виде двух подматриц – информационной I_k и проверочной P. , где ,

Информационную подматрицу часто берут в виде квадратной единичной матрицы:

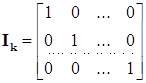
При этом проверочная подматрица P должна строиться с соблюдением следующих условий:

1.вес (количество единиц) каждой строки подматрицы должен быть не менее d_min-1

2. все строки должны быть различны

3.кодовое расстояние между любыми двумя строками подматрицы должно быть не менее d_min-2