Понятие о канальной матрице

Ситуацию с передачей информации по каналу связи с помехами можно описать, используя аппарат марковских цепей.

Посылку в канал в момент времени t_k одного из символов u_i представим как нахождение системы в состоянии i. Всего таких состояний – Nu. Прием из канала в следующий момент времени t_k+1 одного из символов v_j представим как переход системы из состояния iв состояние j. Интервал времени t_k+1-t_k равен средней длительности передачи одного символа τ. Вероятности нахождения системы в состоянии i равны вероятности генерации источником символа u_i. Вероятности перехода за время из состояния i в состояние jравны условной вероятности p(v_j|u_i)принятия символа v_j при условии, что послан символ u_i. Таким образом, функционирование системы на одном шаге описывается вектором начальных вероятностей p(u_i), (i= 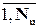), представляющим собой распределение вероятностей символов первичного алфавита, и матрицей переходных вероятностей p(v_j|u_i)размером Nu×Nv.

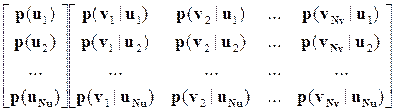
Матрица переходных вероятностей называется канальной матрицей.

Пропускная способность бинарного симметричного канала с помехами типа «инверсия»

Рассмотрим работу достаточно типичной системы связи, в которой информация передается двоичными сигналами «0» и «1», имеющими разные уровни квантования. Приемное устройство анализирует выход канала в течение промежутка времени, соответствующего длительности элементарного сигнала и вычисляет некоторую скалярную величину µ (уровень принятого сигнала). Решение принимается сравнением µ с некоторым порогом ρ. При µ > ρ принимается решение в пользу «1», в противном случае, при µ < ρ, решением будет «0». При правильном выборе порога ρ вероятности ошибок при передаче сигналов будут одинаковыми, и мы приходим к модели бинарного симметричного канала с инверсией (Б.С.К.И.) Недостаток такой простейшей схемы приема состоит в том, что демодулятор теряет информацию о надежности принимаемых сигналов. Очевидно, значениям µ ≈ ρ соответствуют ненадежные решения, и эти сведения могут быть полезными при последующей обработке информации.