Лабораторная работа № 4. Цель работы: исследовать нагрузочную характеристику источника тока и режим его работы в электрических цепях

ИЗУЧЕНИЕ ВЛИЯНИЯ СОПРОТИВЛЕНИЯ НАГРУЗКИ НА НАПРЯЖЕНИЕ, МОЩНОСТЬ, КПД

ИСТОЧНИКОВ ТОКА

Цель работы: исследовать нагрузочную характеристику источника тока и режим его работы в электрических цепях. Научиться определять Э.Д.С. и внутреннее сопротивление источника тока. Определить коэффициент полезного действия источника тока.

Оборудование: источники постоянного тока 0 ¸ 7В, мультиметры, магазин сопротивлений, соединительные провода.

Краткая теория

Рассмотрим отрезок однородного цилиндрического проводника длиной l. Для того, чтобы в этом проводнике шел ток I , необходимо внутри проводника поддерживать постоянное электрическое поле Е. Так как напряженность электрического поля равна градиенту потенциала, взятого с обратным знаком, то

, (4.1.)

где U = j₁ - j₂­ - падение потенциала на участке электрической цепи 1 – 2 ,называемое напряжением.

При изменении напряжения U меняется и ток I. В 1826г. Ом экспериментально установил прямую зависимость между током и напряжением

I ~ U.

Обозначим коэффициент пропорциональности, характеризующий электрическую проводимость проводника, через G; величина R, обратная проводимости проводника, 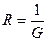называется его электрическим сопротивлением; тогда

(4.2)

Уравнение (7.2) называют законом Ома интегральной форме: ток, идущий в проводнике, численно равен отношению приложенного напряжения к сопротивлению проводника.

Сопротивление проводника зависит от его геометрических размеров и формы, а так же материала, из которого сделан проводник. Для цилиндрических проводников:

, (4.3)

где r - удельное сопротивление вещества.

Подставим (7.3) в (7.2):

и преобразуем к виду

, (4.4)

Величина носит название плотности тока, а - напряженности электрического поля.

Величина, обратная удельному сопротивлению, 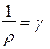, называется удельной проводимостью или электропроводностью данного вещества.

При введенных обозначениях соотношение (4.4) имеет вид:

, (4.5)

и носит название закона Ома в дифференциальной форме.

В ряде случаев на отдельных участках цепи на электрические заряды действуют сторонние силы 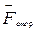, перемещающие на этих участках заряды против направления электрического поля 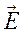. Обозначим через

, (4.6)

При наличии сторонних полей закон Ома в дифференциальной форме примет более общий вид:

, (4.7)

Перейдем от дифференциальных соотношений к интегральным. Рассмотрим замкнутую цепь, на участке 1-2 которой включен сторонний источник тока. Выделим малый элемент тока длиной dl так, чтобы на этом участке можно было считать площадь поперечного сечения проводника S постоянной, а поле и плотность тока - односторонними и направленными перпендикулярно поперечному сечению проводника. Тогда

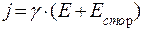, или 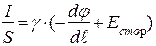, (4.8)

Умножим обе части равенства на r dl = dl /g получаем:

,

Проинтегрируем по участку проводника от 1 до 2:

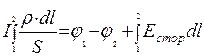, (4.9)

величина представляет собой сопротивление бесконечно малого участка проводника, а - полное сопротивление всего участка цепи. Разность j₁ - j₂ = U_{1, 2} есть падение потенциала на данном участке.

,

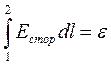носит название Э.Д.С.(электродвижущая сила) источника тока, включенного на этом участке: этот интеграл численно равен работе сторонних сил при переносе по цепи единичного положительного заряда.