в аудиториях № 311 и 315.

Описание установки
Нагреватель находится внутри лабораторного стенда. Внутри нагревателя расположены: термопара(I), медный проводник(II), манганин (III) и полупроводник(IV).
Порядок выполнения работы
1. Соединить клемму «COM» мультиметра М2 с клеммой «Общ.», а клемму «mA, V» M2 с клеммой «I», таким образом термопара будет подсоединена к мультиметру. Переключатель режимов работы мультиметра поставить на измерение температуры. Зафиксировать температуру Т1 (начальная температура спая).
2. Соединить, соблюдая полярность, клеммы источника питания 8,4V с клеммами нагревателя.
3. Переключением режимов работы мультиметра измерить термоэдс при конкретной температуре. (Измерения производить через 3 – 5 0 С). Значения температуры Т2 и соответствующих термоэдс записать в таблицу.
Возможно провести замеры и температуры и термоэдс одновременно. Для этого М1 в режиме измерения температуры, а М2 в режиме измерения напряжения подсоединить к клеммам «Общ.» и «I».
Таблица
| № п/п | T2, °С | e, В | D Т = Т2 - Т1, °С | a, В/°С | ∆a, В/°С | δα % |
| Среднее значение |
11. По формуле (6.2) рассчитать значение α. Значения записать в таблицу. Усреднить значения a и записать среднее значение (αср) в таблицу.
12. Построить график зависимости e(Т) и вычислить значение aграф по тангенсу угла наклона графика.
13. Сравнить полученные значения aграф и αср.
14. Окончательный результат записать в виде:
α = αср ± ∆ αср , 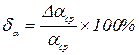 .
.
Контрольные вопросы
1. Что такое термопара (какие виды)?
2. Контактная разность потенциалов (причины возникновения).
3. Эффект Пельтье.
4. Эффект Зеебека.
5. Эффект Томсона.
6. Законы Вольта.
Литература
1. Т. И. Трофимова. Курс физики. М.: Высшая школа, 1997. гл. 9.
2. Б. М. Яворский, А. А. Пинский. Основы физики. М.: Высшая школа, 1974. 1 том,
3. Г. С. Ландсберг. Элементарный учебник физики. М.: ФМЛ, 2 том, 1975 г.
Лабораторная работа № 7.
ИЗМЕРЕНИЕ ЛОКАЛЬНОЙ НАПРЯЖЁННОСТИ МАГНИТНОГО ПОЛЯ
Цель работы: измерение горизонтальной составляющей напряженности магнитного поля в данной точке.
Оборудование: плата с тонкой катушкой, источник питания 0 ÷ 7 В, мультиметр в режиме измерения тока, компас, магазин сопротивления.
Краткая теория
В 1820 г. датский физик Х. Эрстед заметил, что магнитная стрелка поворачивается при пропускании электрического тока через проводник, находящийся около нее. В том же году французский физик А. Ампер установил, что два проводника, расположенные параллельно друг другу, взаимодействуют при пропускании через них электрического тока. На основании этих опытов Ампер пришел к выводу, что взаимодействие тока с магнитом и магнитов между собой можно объяснить, если предположить, что внутри магнита существуют незатухающие молекулярные круговые токи. Тогда все магнитные явления объясняются взаимодействием движущихся электрических зарядов.
Движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Силовой характеристикой магнитного поля служит вектор магнитной индукции. Количественной характеристикой поля служит вектор напряженности магнитного поля. Напряженность не зависит от магнитных свойств среды. В вакууме напряженность магнитного поля совпадает по направлению с магнитной индукцией.
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био и Ф. Саваром. Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био - Савара - Лапласа для проводника с током 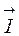 , элемент которого
, элемент которого 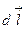 создает в некоторой точке индукцию поля
создает в некоторой точке индукцию поля 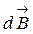 , записывается в виде:
, записывается в виде:
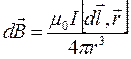 (7.1)
(7.1)
где 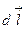 -вектор длины, совпадающий по направлению с током,
-вектор длины, совпадающий по направлению с током, 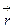 - радиус-вектор, проведенный из элемента dl проводника в точку поля.
- радиус-вектор, проведенный из элемента dl проводника в точку поля.
Магнитное поле в центре кругового проводника с током радиусом r.

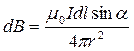 , (7.2)
, (7.2)
где α - угол между векторами 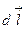 и
и 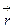 . Так как все элементы проводника перпендикулярны радиус-вектору (sinα =1) и расстояние всех элементов проводника до центра кругового тока одинаково (r), l = 2 π r - длина окружности, μ0=4π.10-7 Гн/м – магнитная постоянная. Тогда выражение (7.2), после интегрирования по поверхности, примет вид:
. Так как все элементы проводника перпендикулярны радиус-вектору (sinα =1) и расстояние всех элементов проводника до центра кругового тока одинаково (r), l = 2 π r - длина окружности, μ0=4π.10-7 Гн/м – магнитная постоянная. Тогда выражение (7.2), после интегрирования по поверхности, примет вид:
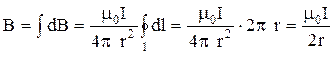 . (7.3)
. (7.3)
Мы получили соотношение для определения магнитной индукции в центре кругового тока.
 Земля представляет собой шаровой магнит, полюса которого располагаются недалеко (~300 км) от географических, только её «южный» магнитный полюс где-то в северном полушарии, около северного географического полюса, а «северный» - в южном. Тогда становится понятным, почему вследствие притяжения этими полюсами разноименных полюсов магнита этот последний устанавливается в направлении, близком к направлению меридиана (рис.7.2). Происхождение магнитного поля Земли связывают с тепловыми движениями проводящего жидкого вещества в земном ядре (Динамо-эффект). В околоземном пространстве магнитное поле образует магнитную ловушку для заряженных частиц высоких энергий - радиационный пояс. Лишь в полярных областях небольшая часть этих частиц вторгается в верхние слои атмосферы и вызывает полярные сияния. Из других планет Солнечной системы лишь Юпитер и Сатурн собственными магнитными полями, достаточными для создания устойчивых планетарных магнитных ловушек. Через магнитные полюса можно провести магнитные меридианы, в первом приближении представляющие окружности, параллельные земной поверхности. Магнитная стрелка компаса в отсутствие искажающих масс магнетиков или токов, вращающаяся в горизонтальной плоскости устанавливается в плоскости магнитного меридиана под действием магнитного поля земли. При этом говорят о магнитном склонении - угле между направлениями географического и магнитного меридиана.
Земля представляет собой шаровой магнит, полюса которого располагаются недалеко (~300 км) от географических, только её «южный» магнитный полюс где-то в северном полушарии, около северного географического полюса, а «северный» - в южном. Тогда становится понятным, почему вследствие притяжения этими полюсами разноименных полюсов магнита этот последний устанавливается в направлении, близком к направлению меридиана (рис.7.2). Происхождение магнитного поля Земли связывают с тепловыми движениями проводящего жидкого вещества в земном ядре (Динамо-эффект). В околоземном пространстве магнитное поле образует магнитную ловушку для заряженных частиц высоких энергий - радиационный пояс. Лишь в полярных областях небольшая часть этих частиц вторгается в верхние слои атмосферы и вызывает полярные сияния. Из других планет Солнечной системы лишь Юпитер и Сатурн собственными магнитными полями, достаточными для создания устойчивых планетарных магнитных ловушек. Через магнитные полюса можно провести магнитные меридианы, в первом приближении представляющие окружности, параллельные земной поверхности. Магнитная стрелка компаса в отсутствие искажающих масс магнетиков или токов, вращающаяся в горизонтальной плоскости устанавливается в плоскости магнитного меридиана под действием магнитного поля земли. При этом говорят о магнитном склонении - угле между направлениями географического и магнитного меридиана.
Кроме того, для характеристики вертикальной составляющей вводят магнитное наклонение - угол между направлением вектора напряженности магнитного поля и горизонтальной плоскостью.
Наклонение может быть южным или северным (южный или северный конец стрелки ниже горизонтальной плоскости). Эти два угла называют элементами земного магнетизма.
Магнитная стрелка устанавливается в плоскости магнитного меридиана под действием вектора индукции магнитного поля, но в силу установившихся традиций обычно говорят о векторе напряженности. Реально магнитное поле в современных условиях города представляет суперпозицию полей искусственного происхождения и искаженно большими массами ферромагнетиков (арматура, центральное отопление и т. д.)
В данной работе измерение горизонтальной составляющей земного магнитного поля основывается на принципе суперпозиции (наложения) магнитных полей.
При помощи компаса определяют направление земного горизонтального поля 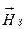 . Затем создают добавочное магнитное поле с известной напряженностью
. Затем создают добавочное магнитное поле с известной напряженностью 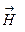 .
.
С помощью компаса определяют направление результирующего 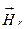 поля, которое по принципу суперпозиции будет равно векторной сумме этих полей:
поля, которое по принципу суперпозиции будет равно векторной сумме этих полей:


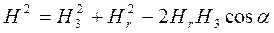 .
.
Для простоты расчета добавочное магнитное поле создают перпендикулярным земному, тогда:
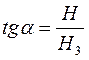 .
.
Поле кругового тока можно вычислить, зная ток I по формуле (7.3), учитывая, что В = μ μ0 Н :
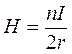 , (7.4)
, (7.4)
где n - число витков, r - радиус тонкой катушки, отсюда
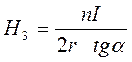 (7.5)
(7.5)
Схема установки
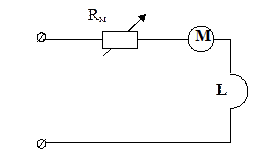
Rм – магазин сопротивления;
L – плата с катушкой;
М – мультиметр в режиме амперметра.
Порядок выполнения работы
1. Закрепляют панель с катушкой на верхней части стола, ориентируя ось катушки по компасу (стрелка компаса должна располагаться вдоль витков катушки).
2. Собирают схему установки. Измеряют радиус катушки (r), число витков (n) указано на катушке. Записать их в таблицу.
3. Устанавливают с помощью магазина сопротивление R=10 Ом и включают блок питания 0÷7В.
4. Увеличением напряжения добиваются, чтобы стрелка отклонилась на произвольный угол α1 при этом, записывают значения тока и угла в таблицу.
Таблица
| α1(град) | a2(град) | I (А) | αср= (a1+a2)/2 | ctg αср | Hз (А/м) | |
| r = | n = | Hз ср. = |
5. Чтобы избежать возможной не параллельности стрелки магнитному меридиану меняют полярность питания катушки и фиксируют значение угла α2 при неизменном подаваемом напряжении и токе.
6. По полученным значениям углов α1 и α2, рассчитывают среднее значение угла αср при данном подаваемом напряжении и токе:
αср =(α1+α2)/2
7. Проделывают опыт несколько раз для различных значений тока I и выводят среднее значение Нз по формуле (7.5).
8. Рассчитать абсолютную и относительную погрешности при косвенном измерении величины Нз.
Контрольные вопросы
1. Что характеризуют вектора магнитной индукции и напряженности магнитного поля?
2. Выведите формулу магнитной индукции в центре кругового проводника с током.
3. Каковы элементы земного магнетизма?
4. Выведите расчетную формулу (7.5).
Литература
1. Калашников C.Г. Электричество. М.: Наука, 1985. гл.8.
2. Яворский Б.М., Детлаф А.А. Курс физики. М.: Высшая школа, 1983. т.2, гл.7.
3. Сорокин А.Ф., Сурков М.И., Кушкин С.А. Руководство к лабораторным работам по физике. Астрахань 1997.
Лабораторная работа № 8.
Измерение удельного заряда электрона и изучение силы Лоренца.
Цель: изучить движение заряженных частиц в электромагнитном поле.
Оборудование: осциллограф с встроенным соленоидом, источник переменного тока 0 ÷ 7 В, соединительные провода, мультиметр в режиме амперметра.
Краткая теория
Магнитное поле – форма существования материи, обладающая свойством передавать магнитное взаимодействие.
Магнитное поле порождается только движущимися зарядами. Основной характеристикой магнитного поля является 
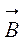 (магнитная индукция) – физическая величина, численно равная максимальному вращательному моменту, действующему на пробный контур с единичным магнитным моментом, помещенным в данную точку поля.
(магнитная индукция) – физическая величина, численно равная максимальному вращательному моменту, действующему на пробный контур с единичным магнитным моментом, помещенным в данную точку поля.
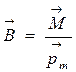 , (8.1)
, (8.1)
где 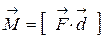 - механический момент контура с током,
- механический момент контура с током,  - магнитный момент контура площадью S.
- магнитный момент контура площадью S.
В данной работе изучается действие на движущуюся заряженную частицу со стороны магнитного поля. Силу этого воздействия называют силой Лоренца и определяют по формуле:

Fл = 
 (8.2)
(8.2)
где q - заряд, V - скорость частицы.
Направление силы Ампера определяется правилом левой руки (рис. 8.1):
1) направление линий магнитной индукции входят в левую ладонь;
2) четыре пальца вытянуты по направлению тока;
3) отогнутый на 900 большой палец указывает направление силы Ампера.
Сила Лоренца определяется аналогично (учитывая, что четыре пальца вытянуты по направлению скорости движения положительного заряда).
Характер движения частицы в однородном поле зависит от угла α между направлением скорости и индукции магнитного поля.
 I.
I. 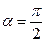 . Скорость заряда перпендикулярна магнитной индукции, сила Лоренца имеет максимальное значение
. Скорость заряда перпендикулярна магнитной индукции, сила Лоренца имеет максимальное значение 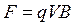 и направлена перпендикулярно скорости и индукции. Эта сила создает центростремительное ускорение и заставляет электрон двигаться по окружности в плоскости, перпендикулярной к индукции (рис. 8.2).
и направлена перпендикулярно скорости и индукции. Эта сила создает центростремительное ускорение и заставляет электрон двигаться по окружности в плоскости, перпендикулярной к индукции (рис. 8.2).
II. α = 0. Скорость заряда параллельна магнитной индукции, тогда 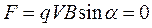 , магнитное поле никакого действия на заряд не оказывает.
, магнитное поле никакого действия на заряд не оказывает.
 III.
III. 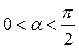 . Скорость заряда направлена под острым углом к магнитной индукции (рис. 8.3), тогда скорость движения электрона можно разложить на две составляющие, одна из которых Vn перпендикулярна, а другая Vτ параллельна магнитному полю.
. Скорость заряда направлена под острым углом к магнитной индукции (рис. 8.3), тогда скорость движения электрона можно разложить на две составляющие, одна из которых Vn перпендикулярна, а другая Vτ параллельна магнитному полю.
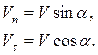 (8.3)
(8.3)
Перепишем (8.2) в скалярной форме: 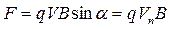 (8.4)
(8.4)
Таким образом, на величину силы Лоренца, помимо величины поля, влияет только нормальная составляющая скорости. Справедливо и обратное утверждение – сила Лоренца изменяет только нормальную составляющую скорости (почему?). Рассматривая движение электрона как сложное со скоростями Vn и Vτ , можно утверждать, что сила Лоренца не влияет на движение вдоль поля (движение по прямой) и является причиной изменения направления нормальной составляющей скорости (движение по окружности). Результирующее движение будет движением по винтовой линии (рис. 8.3).
Для движения электрона по окружности (в плоскости перпендикулярной к магнитной индукции) сила Лоренца является центростремительной:
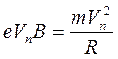 . (8.5)
. (8.5)
Тогда время одного полного оборота с учетом (8.5) равно:
 (8.6)
(8.6)
За время одного оборота электрон, участвуя в равномерном и прямолинейном движении вдоль поля, сместится в этом направлении на расстояние, равное шагу винта h (смещение электрона за время, равное периоду) (рис. 8.3):
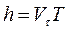 . (8.7)
. (8.7)
Из (8.3), (8.6), (8.7) следует, что:
 (8.8)
(8.8)
Рассмотрим важный для практики случай, когда углы α малы (α<<1). Тогда:
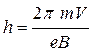 . (8.9)
. (8.9)
Таким образом, путь h, пройденный электроном в магнитном поле за один оборот, не зависит от угла α (для малых углов). Поэтому все электроны, вышедшие из одной точки в разных направлениях под небольшими углами к магнитному полю, после одного оборота вновь соберутся в одной точке. В этом заключается принцип магнитной фокусировки электронов. Соотношение (8.9) может служить для определения удельного заряда электрона ( 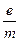 ): (учтем: e = q )
): (учтем: e = q )
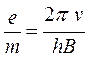 . (8.10)
. (8.10)
Для осуществления эксперимента электроны разгоняются в электрическом поле с разностью потенциалов U и приобретают кинетическую энергию:
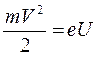 (8.11)
(8.11)
Решая совместно (8.10) и (8.11), можно найти:
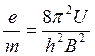 (8.12)
(8.12)
Удельный заряд является важной характеристикой элементарных частиц, знание которой необходимо при расчете конструкций электровакуумных приборов, электронно-оптических установок, ускорителей элементарных частиц разного типа, широко применяемых в современной науке и технике. Экспериментальные методы определения удельного заряда основаны на законах движения электронов в электрических и магнитных полях. Эти же методы применяются для определения массы частицы, если известен её заряд, или заряда при известной массе.
Наиболее точное значение удельного заряда электрона, установленное с учетом результатов, полученных различными методами, равно:
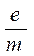 = 1,76*1011Кл/кг.
= 1,76*1011Кл/кг.
Описание метода эксперимента
За время полета 
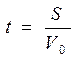 электронов они поворачиваются
электронов они поворачиваются
на угол j: j 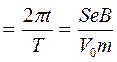 ,
,
который не зависит от скорости 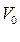 .
.
На экране осциллографа в этом случае линии развертки поворачивается на этот угол j . Измерение:
tg j = U / C (8.13)
позволяет найти удельный заряд электрона из соотношения:
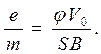 (8.14)
(8.14)
По закону сохранения энергии :
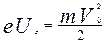 , (8.15)
, (8.15)
откуда выразим V0 :
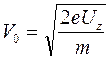 . (8.16)
. (8.16)
Подставим (8.16) в ( 8.15 ), получим :
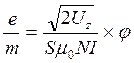 , (8.17)
, (8.17)
где m0 NI = B, m0 = 4p ´ 10 -7 Гн / м,
N - число витков соленоида,
I - ток в соленоиде,
Uz ~ 1.25´ 103 В.
Обозначим постоянную величину :
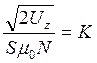 . (8.18)
. (8.18)
Ее определяют индивидуально для каждой установки. Окончательно получаем:
 . (8.19)
. (8.19)
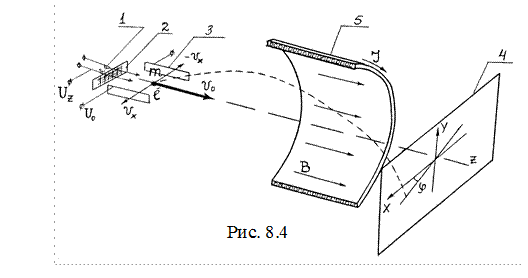
1) Катод; 2) Управляющая сетка; 3) Пластины горизонтальной развертки; 4) Экран; 5) Соленоид.
Для изучения силы Лоренца на клеммы МП, обозначающие выводы соленоида, на боковой поверхности осциллографа, подают напряжение, с источника постоянного тока (0÷7В) включая последовательно с соленоидом мультиметр для измерения силы тока. При протекании электрического тока по соленоиду, возникающее магнитное поле действует на электроны, если они имеют отличную от нуля составляющую скорости, перпендикулярную оси соленоида Vx с силой:
F= eBVx..
Величина Vx задается пилообразным напряжением развертки луча осциллографа, подаваемым на пластины горизонтального отклонения 3 (рис.8.4). Электроны испускаются накаленной нитью 1 (катод) и ускоряются напряжением сетки 2. Так как ускоряющая разность потенциалов Uz ~ 1.25´ 103 В много больше напряжения на отклоняющих пластинах U0 ~ 100 В, можно считать, что продольная скорость у всех электронов в данный момент одинакова. Электроны с разными поперечными скоростями в разные моменты времени по развертке попадают в разные точки экрана и создают изображение прямой линии вдоль оси X. При включении поля электроны двигаются по спирали.
Порядок выполнения работы
1. Собрать электрическую схему: подключить мультиметр в режиме измерения силы тока последовательно с соленоидом (1 клемма соленоида расположена на боковой стороне осциллографа, а 2- земля) к источнику постоянного тока 0 ¸ 7 В.
2. Включить ток через обмотку соленоида и наблюдают наклон горизонтальной развертки луча осциллографа. Меняя полярность источника тока, меняется угол наклона луча на противоположный, что свидетельствует о векторном характере силы Лоренца.
3. При нескольких значениях тока I рассчитывают угол j по формуле (8.13), замеряя X и Y ( не менее 5 раз ) и заносят результат в таблицу.
Таблица
| № п/п | 2х ( мм) | Y(мм ) | j (град) | I(А) | e/m (Кл/кг) | De/m (Кл/кг) | Ee/m % |
| Среднее значение |
4. Рассчитать значение 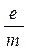 по формуле (8.19), используя значение К, вычисленного по формуле (8.18), где N – число витков соленоида (спросить у преподавателя).
по формуле (8.19), используя значение К, вычисленного по формуле (8.18), где N – число витков соленоида (спросить у преподавателя).
5. Вычислить значение абсолютной и относительной ошибки
измерения e/m.
Контрольные вопросы
1. Магнитное поле (его источник, основная характеристика).
2. Сила Лоренца (от чего зависит, на что действует, как определяется направление?).
3. Как зависит характер движения частицы в однородном поле от угла α между направлением скорости и индукции магнитного поля.
4. Шаг винтовой линии (определение, вывод формулы 8.9)
5. Что такое удельный заряд электрона? Чему он равен? (вывод формулы 8.12).
6. Описать метод эксперимента с выводом расчетной формулы (8.19).
Литература
5. Зисман Г. А. Тодес О. М. Курс общей физики. Т.2, гл.VII. 1974.
6. Детлаф А. А. Яворский Б. М. Курс физики. 1989 г. стр. 208 – 209.
7. Савельев И.В. Курс общей физики. Т. 2, гл. 10.М.: Наука, 1978 г.,
8. Детлаф А. А. Яворский Б. М. Справочник по физике. гл. VII. М.: ФМЛ, 1963 г.,
9. Кушкин С.А., Сорокин А.Ф., Сурков М.И. Руководство к лабораторным работам по физике. А: 1997.
Лабораторная работа № 9.
ИЗУЧЕНИЕ РАБОТЫ ПОЛУПРОВОДНИКОВОГО ДИОДА.
Цель работы: изучение (экспериментально) вольтамперной характеристики полупроводникового диода.
Оборудование: источник питания 0÷7 В, диод, мультиметр (2 шт.), провода соединительные.
Краткая теория
Электронные состояния в кристаллах образуют энергетические зоны. Связанные состояния образуют валентную зону, свободные – зону проводимости. Полупроводниками называются кристаллы, для которых энергетическая щель между этими зонами DW лежит в пределах 0 < DW < 2 эВ. Полупроводниковые материалы объединяют обширный класс материалов с удельным сопротивлением 10-8÷10-6 Ом·м. Наиболее типичными полупроводниками являются кремний (Si) и германий (Ge).Чистые полупроводники обладают всегда равным числом электронов в зоне электронной проводимости и дырок. Обычно эти полупроводники называются полупроводниками с собственной проводимостью или собственными полупроводниками. Особую роль в физике и технике играют, однако, так называемые примесные полупроводники. Ничтожные количества примесей резко меняют электрические свойства полупроводников. При этом примесью обычно для краткости называют не только наличие атомов других элементов, нарушающих правильность кристаллической решетки, но и любые ее нарушения: наличие атома того же элемента, находящегося не в узле, а в междоузлии решетки, либо отсутствие атома в узле. В дальнейшем для определенности мы будем рассматривать нарушения решетки, обусловленные наличием реальных примесей - атомов других элементов.
Наличие примесных атомов сказывается на поведении полупроводника двояко. Если, например, в кристаллической решетке чистого четырехвалентного полупроводника германия один из атомов заместить атомом пятивалентной сурьмы, то последний легко отдаст лишний пятый электрон. В той же решетке атом трехвалентного индия, заместивший один из атомов германия, будет стремиться присоединить к себе четвертый электрон.
Примеси, отдающие электроны, называются донорными; примеси, стремящиеся присоединить к себе электроны - акцепторными. Таким образом, атомы сурьмы в кристаллической решетке германия являются донорами, атомы индия - акцепторами.
 Рассмотрим конкретный пример. На (рис.9.1.а) изображена плоская схема кристалла германия. Германий четырехвалентен. Это значит, что во внешней оболочке его атомов имеются четыре слабо связанных электрона, которые осуществляют связь между данным и соседними атомами. На схеме эти связи показаны пунктирными стрелками.
Рассмотрим конкретный пример. На (рис.9.1.а) изображена плоская схема кристалла германия. Германий четырехвалентен. Это значит, что во внешней оболочке его атомов имеются четыре слабо связанных электрона, которые осуществляют связь между данным и соседними атомами. На схеме эти связи показаны пунктирными стрелками.
 Заместим теперь один из атомов германия каким-нибудь пятивалентным атомом (сурьма, мышьяк). Из пяти электронов внешней оболочки атома примеси четыре будут вести себя, как электроны атома германия. Пятый же электрон окажется свободным. Таким образом, атом примеси превратится в положительный ион (рис.9.1.б). При отсутствии добавочных взаимодействий свободный электрон будет удерживаться вблизи положительного иона. Однако их связь будет слаба, и под действием уже небольшого поля этот электрон сможет перемещаться против него, участвуя тем самым в электронной проводимости кристалла.
Заместим теперь один из атомов германия каким-нибудь пятивалентным атомом (сурьма, мышьяк). Из пяти электронов внешней оболочки атома примеси четыре будут вести себя, как электроны атома германия. Пятый же электрон окажется свободным. Таким образом, атом примеси превратится в положительный ион (рис.9.1.б). При отсутствии добавочных взаимодействий свободный электрон будет удерживаться вблизи положительного иона. Однако их связь будет слаба, и под действием уже небольшого поля этот электрон сможет перемещаться против него, участвуя тем самым в электронной проводимости кристалла.
 Пусть, например, в рассмотренную выше решетку германия введены атомы трехвалентного индия (рис.9.1.в), во внешней оболочке которых имеются три электрона. Вследствие структуры решетки, атом индия должен будет стремиться к захвату еще одного электрона, которым может быть один из свободных электронов (по принятой выше терминологии - электрон из зоны электронной проводимости). Таким образом, электроны, которые при отсутствии примеси были бы свободны, «оседают» на атомах акцептора и подвижностью будут обладать главным образом дырки.
Пусть, например, в рассмотренную выше решетку германия введены атомы трехвалентного индия (рис.9.1.в), во внешней оболочке которых имеются три электрона. Вследствие структуры решетки, атом индия должен будет стремиться к захвату еще одного электрона, которым может быть один из свободных электронов (по принятой выше терминологии - электрон из зоны электронной проводимости). Таким образом, электроны, которые при отсутствии примеси были бы свободны, «оседают» на атомах акцептора и подвижностью будут обладать главным образом дырки.
В зависимости от механизма проводимости мы будем называть такие полупроводники электронными или дырочными и обозначать соответственно буквами n (от слова «negativ», что означает отрицательный знак подвижного заряда) или р (от слова «positiv»—положительный).
Электропроводность полупроводников резко увеличивается с ростом температуры. При этом электроны переходят из занятой валентной зоны, где образуются «дырки», в ранее пустовавшую зону, где образуются «электроны проводимости».
Полная электропроводность проводников является суммой дырочной (p-проводимость) и электронной (n-проводимость) электропроводности.
 Полупроводниковый диод представляет собой контакт полупроводников n-типа и p-типа. В области контакта электроны и дырки нейтрализуют друг друга (рекомбинируют) и концентрация носителей тока становится очень малой. Возникает слой с большим сопротивлением, «запорный» слой или слой p-n перехода.
Полупроводниковый диод представляет собой контакт полупроводников n-типа и p-типа. В области контакта электроны и дырки нейтрализуют друг друга (рекомбинируют) и концентрация носителей тока становится очень малой. Возникает слой с большим сопротивлением, «запорный» слой или слой p-n перехода.
Диод обладает односторонней проводимостью, то есть его сопротивление меняется в тысячи раз в зависимости от полярности приложения напряжения. Рассмотрим причину происходящего явления. Присоединим к кристаллу стороннюю э.д.с. так, как это показано на (рис.9.2.а): минус - к n-кристаллу и плюс – к р- кристаллу (прямое подключение). Внешнее поле будет уменьшать поле, созданное в области контакта, т. е. облегчит передвижение свободных носителей заряда в этой области. Ток через кристалл будет сравнительно большим.
 Переменим теперь полюсы внешней э.д.с. (обратное подключение) (рис.9.2. б). В этом случае внешнее поле в области контакта действует так же, как и внутреннее, т. е. обедняет ее подвижными носителями заряда. Сопротивление этой области сильно возрастает, ток проводимости резко уменьшается. При данном напряжении внешнего источника э.д.с. прямой ток в десятки и сотни раз превышает обратный ток.
Переменим теперь полюсы внешней э.д.с. (обратное подключение) (рис.9.2. б). В этом случае внешнее поле в области контакта действует так же, как и внутреннее, т. е. обедняет ее подвижными носителями заряда. Сопротивление этой области сильно возрастает, ток проводимости резко уменьшается. При данном напряжении внешнего источника э.д.с. прямой ток в десятки и сотни раз превышает обратный ток.
 Так как сопротивление полупроводникового диода зависит от полярности и величины приложенного напряжения, то его вольт амперная характеристика становится не линейной. Эта нелинейность и обуславливает практическое использование диода в качестве выпрямителя, ограничителя и демодулятора электрических сигналов. Типичная вольтамперная характеристика диода представлена на рис.9.3.
Так как сопротивление полупроводникового диода зависит от полярности и величины приложенного напряжения, то его вольт амперная характеристика становится не линейной. Эта нелинейность и обуславливает практическое использование диода в качестве выпрямителя, ограничителя и демодулятора электрических сигналов. Типичная вольтамперная характеристика диода представлена на рис.9.3.
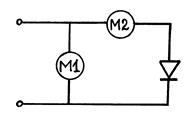
Схема установки
Ход работы
1. Собрать схему установки, используя источник 0÷7 В; М1 – мультиметр в режиме вольтметра; М2 – мультиметр в режиме миллиамперметра (mA) – для прямого включения диода, и в режиме микроамперметра (μА) – для обратного.
2. Регулируя, подаваемое с источника напряжение, записать показания амперметра и вольтметра в таблицу (для прямого и обратного подключений диода). Необходимо сделать не менее 10 замеров.
3. Построить графики зависимостей I(U) для прямого и обратного включений.
Переход от прямого подключения диода к обратному (или наоборот) можно осуществить, поменяв полярность подключения источника.
Таблица
| Прямой ток | Обратный ток | ||
| U, В | I, mА | U, В | I, μА |
Дата добавления: 2015-09-11; просмотров: 657;
