Поняття пружинного і математичного маятника, формули періодів їх коливань
Якщо розтягнути і відпустити закріплену одним кінцем пружину, її коливання будуть дуже короткочасними внаслідок малої маси пружини. Для збільшення інертності коливальної системи до пружини прикріплюють тягарець масою m. Під дією його сили тяжіння пружина видовжується. Положення центра тяжіння тягарця О — положення рівноваги майбутніх коливань такої системи.
З виразу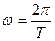 
одержимо: 
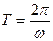; тому формули періодів коливань будь-яких систем мають однаковий початок: Т=2 
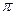...; виявилось також, що у правій частині всіх формул Т є множник під корнем:
.
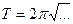"... Олександр Якович ("блакитний злодійчук") забезпечив всі двері пружинами найрізноманітніших систем і фасонів.... пружини мали могутню силу. Двері зачинялись з такою ж стрімкістю, як дверці мишоловок" (І. Ільф, Є. Петров "12 стільців") (Олександр Якович "знав" фізику).
Отже: чим більша жорсткість пружини к, тим менший період її коливань. Очевидно також, що чим більша маса тягарця т, тим більший період коливань.
(Система більшої маси поводить себе "солідно": не поспішає, "не частить".)
Остаточно: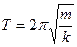 
.
"Небезпечний експеримент": "Моє тіло лежало під прямим кутом до площини, в якій розгойдувався маятник; його нижня частина являла собою сталевий півмісяць, лезо його здавалось гострим мов бритва. Мій зір супроводжував зльоти і падіння маятника" (Едгар По "Колодязь і маятник").
Математичний маятник — це тіло типу матеріальної точки, підвішене на довгій невагомій нерозтяжній нитці.
При відхиленні нитки від вертикального положення система може здійснювати коливання у вертикальній площині під дією повертаючої Сили F1
(складової сили тяжіння FТ).
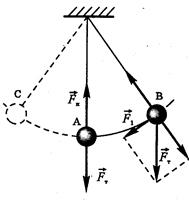
а) T тим більше, чим більше l (тягарець на довгій нитці коливається "не поспішаючи").
б) T тим менше, чим менше Fт (на Місяці коливання маятника були б більш повільними, ніж на Землі). Навіть без виведення, з міркувань розмірності випливає, що у формулі періоду коливань під знаком "квадратного кореня" повинна бути не Fт, а її прискорення £.
Отже: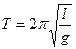 
Дата добавления: 2015-09-11; просмотров: 834;