Ідея роботи та виведення робочої формули.

Період коливання фізичного маятника описує формула

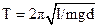,(1)

де І – момент інерції маятника відносно осі, що проходить через точку його підвісу, m – маса маятника, d – відстань від точки підвісу до центра мас маятника, g – прискорення вільного падіння (рис.2).

Як відомо, період коливання математичного маятника описує формула

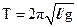, (2)

де l– довжина нитки підвісу математичного маятника.

Довжину такого марема-тичного маятника, який має однаковий період із даним фізичним маятником, називають зведеною довжиною фізичного маятника.

Прирівнявши (1) і (2), отримаємо вираз для зведеної довжини фізичного маятника

l = I / md (3)

На практиці зведену довжину фізичного маятника визначають віддалю між точкою підвісу маятника і його центром коливання. Ці дві точки лежать на одній прямій із центром мас маятника та розміщені по обидва боки від нього. Точки мають властивість спряженості, тобто, якщо перевернути маятник і його центр коливання зробити точкою підвісу, то попередня точка стане центром коливання, а період коливання маятника матиме попереднє значення.

Знайшовши дві такі точки, навколо яких маятник коливається з однаковим періодом, і вимірявши період та відстань між цими точками, можна за формулою (2) визначити прискорення вільного падіння:

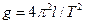. (4)

Оскільки домогтися повної однаковості періодів дуже важко, то Бесель довів, що прискорення g можна отримати простіше i з тією ж точністю, якщо періоди коливань маятника в прямому й оберненому положеннях збігаються лише приблизно.

Нехай маятник підвішений у прямому положенні, тоді період його коливань

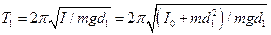, (5)

де І₀ – момент інерції маятника відносно осі, яка проходить через його центр мас, d₁ – відстань від точки підвісу до центра мас маятника, а I=I₀+md₁² згідно теореми Штейнера.

Якщо маятник підвісити в оберненому положенні, то

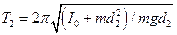. (6)

У формулах (5) i (6) d₁ і d₂ – відстані від центра мас маятника до першої i другої призм, причомуd₁ + d₂=l– відстань між призмами.

Тепер зведемо формули (5) та (6) до вигляду

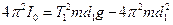; (7)

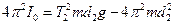(8)

і прирівняємо праві частини цих рівнянь, урахувавши, що l=d₁+d₂. Звідси отримаємо робочу формулу

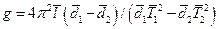(9)