Лабораторна робота 116. ДОСЛІДНА ПЕРЕВІРКА ТЕОРЕМИ ГЮЙГЕНСА-ШТЕЙНЕРА

Завдання: дослідним шляхом перевірити теорему Гюйгенса-Штейнера.

Приладдя: штатив із пружним підвісом, симетричний фізичний маятник, тіла правильної геометричної форми (диск, трикутна та квадратна пластини), секундомір, технічна вага з набором важків, штангенциркуль.

Теоретичний матеріал: момент сили, момент інерції матеріальної точки та твердого тіла, момент імпульсу, рівняння моментів (основний закон динаміки обертального руху), теорема Гюйгенса-Штейнера, моменти інерції тіл правильної геометричної форми, фізичний маятник, крутильні коливання, період коливань фізичного та крутильного маятників.

Література:

1. Р.4. §§. 4.1 - 4.3; Р.10. §.10.5;

2. Р.4. §.§. 4.2, 4.4 – 4.6; Р.8. §. 8.5;

3. §§. 9.1 – 9.7;

4. §. 36 - 40; §. 64;

5. §. 32 §.34.

Опис установки.Лабораторна установка складається зі штатива 3, до якого прикріплені два крон-штейни (див. рисунок). Перший кронштейн закін-чується вилкою із заглибиною, в яку встав-ляють ребро металевої призми фізичного маят-ника 1. До другого кронштейна прикріп-лений пружний підвіс 2 (сталева дротина), нижній кінець якої закінчується стержнем з гайкою. Справедливість теореми Гюйгенса-Штейнера перевіряють за допомогою фізичного маятника, що є однорідним стержнем, на кінцях якого симетрично до його центра мас (отвору в стержні) запресовані металеві тригранні призми. Підвішуючи на вилку першого кронштейна фізичний маятник, можна визначити його момент інерції відносно осі, яка проходить через ребро однієї з металевих призм, а прикріпивши маятник до пружного підвісу методом крутильних коливань можна визначити його момент інерції відносно осі, яка проходить через центр мас і є паралельною до попередньої осі.

Виведення робочих формул. Період коливань фізичного маятника (див. роботу 115) визначають з формули

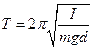, (1)

де 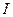– момент інерції маятника відносно осі його підвісу; 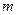– маса маятника; – прискорення вільного падіння; – відстань від осі підвісу до центра мас маятника.

Отже, вимірявши період коливань фізичного маятника 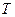, його масу 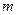та відстань , можна обчислити момент інерції за формулою

. (2)

Момент інерції цього маятника відносно осі, яка проходить через його центр мас і паралельна до попередньої, можна експериментально визначити, застосовуючи крутильні коливання. Відомо (див. роботу 120), що період крутильних коливань

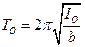, (3)

де 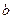– модуль кручення підвісу.

З формули (3)

. (4)

Щоб вилучити невідомий модуль кручення підвісу 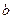, додатково вимірюють період 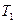крутильних коливань тіла правильної геометричної форми, момент інерції 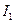якого можна обчислити, знаючи масу і розміри. Аналогічно до формули (4) момент інерції додаткового тіла

. (5)

З формул (4) і (5)

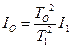. (6)

Якщо допоміжним тілом є диск, то його момент інерції відносно осі симетрії, перпендикулярної до його площини,

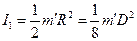, (7)

де 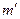–маса диска, – його діаметр.

Для квадратної пластинки, відповідно: , (8)

де – довжина сторони квадрата.

Для трикутної пластинки: , (9)

де 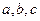– сторони трикутника.

Згідно з теоремою Гюйгенса-Штейнера момент інерції тіла 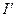відносно довільної осі обертання дорівнює моментові інерції відносно паралельної осі, яка проходить через центр мас тіла, доданому до добутку маси тіла на квадрат відстані між осями:

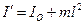. (10)

Цю теорему перевіряємо так. Підставимо у формулу (10) вираз (6) і обчислимо значення 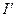. Порівняємо це значення з обчисленим на підставі експерименту за формулою (2) значенням 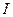, тобто . (11)