Формула Шеннона (мера Шеннона).
Базируясь на вероятностном подходе к оцениванию информации, К.Шеннон в 1948 году вывел формулу, которая дает оценку информации, абстрагируясь от ее содержания:
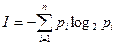 (1.9)
(1.9)
где 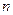 - число состояний системы,
- число состояний системы, 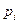 - вероятность, или относительная частота перехода системы в
- вероятность, или относительная частота перехода системы в 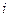 -ое состояние,
-ое состояние,  - количество информации в битах, которую дает, в среднем, появление одного из
- количество информации в битах, которую дает, в среднем, появление одного из 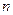 разновероятных состояний системы. Таким образом,
разновероятных состояний системы. Таким образом,
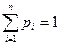 .
.
Формулу Шеннона можно получить на основе следующего мыслительного эксперимента. Пусть есть программа-генератор, которая на экране дисплея может демонстрировать любую букву некоторого алфавита, который состоит из 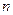 букв.
букв.
| ai | a1 | a2 | a3 | . . . | an |
| pi | p1 | p2 | p3 | . . . | pn |
Генерирование осуществляется соответственно заданным законам распределения. Каждая из букв появляется на экране согласно с вероятностью ее появления pi. За экраном дисплея ведется наблюдение: пусть на экране появилось m букв (m – довольно большое число, значительно больше чем 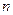 ). Если интересует буква ai, то она на экране появится приблизительно
). Если интересует буква ai, то она на экране появится приблизительно 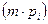 раз. Каждое появление на экране буквы ai дает по формуле (1.7) количество информации, которая равняется
раз. Каждое появление на экране буквы ai дает по формуле (1.7) количество информации, которая равняется 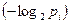 , всего (за все ее появления) на экране будет получено
, всего (за все ее появления) на экране будет получено 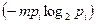 битов информации. Общее количество информации, которое необходимо просуммировать после демонстрации всех m букв, равняется
битов информации. Общее количество информации, которое необходимо просуммировать после демонстрации всех m букв, равняется
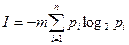 .
.
На одну букву в среднем приходится:
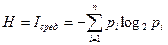 (1.10)
(1.10)
Из этой формулы, как частный случай, получается формула Хартли (1.6). Действительно, если каждое состояние системы является равновероятным, т.е. 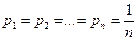 , то энтропия системы будет максимальной и равняется:
, то энтропия системы будет максимальной и равняется: 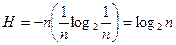 .
.
Дата добавления: 2015-09-11; просмотров: 742;
