Измерение количества информации по Р.Хартли.
Меру количества информации установил в 1928 году Р.Хартли на основе предложенной им концепции выбора. Согласно этой концепции связь между отправителем и получателем информации осуществляется только при наличии определенного набора сообщений, из которых отправитель в каждый момент времени выбирает только одно. В результате последовательных выборов вниманию получателя предлагается последовательность сообщений (символов). Во время каждого выбора исключаются все другие сообщения (символы), которые могли бы быть выбраны.
Пусть сообщение состоит из 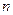 элементов, которые последовательно и независимо выбирают из
элементов, которые последовательно и независимо выбирают из 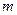 равновероятных элементов. Число возможных сообщений в этом случае (по теореме 1):
равновероятных элементов. Число возможных сообщений в этом случае (по теореме 1):
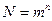 (1.3)
(1.3)
Хартли установил, что в роли меры количества информации, которая имела бы практическую ценность, лучше выбрать не число  , а логарифм этого числа:
, а логарифм этого числа:
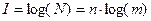 (1.4)
(1.4)
Мера количества информации, введенная Хартли, целиком согласуется с природными интуитивными требованиями к такой мере. Прежде всего, интуитивно ощущается, что количество информации в сообщении будет тем больше, чем длиннее сообщение: например, более длинная телеграмма содержит и больше сведений. Кроме этого, характеристика какого-нибудь явления будет тем лучше, чем большую разновидность сообщений о нем можно использовать. Например, оценка студента по 100-бальной системе лучше отражает его знания, чем пятибальная.
Формула (1.3) отображает и зависимость количества информации от длины сообщения 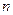 и от разнообразия элементов в сообщении
и от разнообразия элементов в сообщении 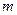 . Следует отметить: для вывода формулы (1.4) Хартли сделал предположение, что элементы сообщения равновероятны и выбор каждого элемента осуществляется независимо от того, какие элементы были раньше выбраны. В информметрии идеи Хартли интерпретируются с более общей позиции, которая вытекает из понятия системы.
. Следует отметить: для вывода формулы (1.4) Хартли сделал предположение, что элементы сообщения равновероятны и выбор каждого элемента осуществляется независимо от того, какие элементы были раньше выбраны. В информметрии идеи Хартли интерпретируются с более общей позиции, которая вытекает из понятия системы.
Пусть есть система 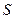 из
из  равновероятных (равновозможных) состояний. Если каждое состояние системы закодировать равномерным кодом определенной длины
равновероятных (равновозможных) состояний. Если каждое состояние системы закодировать равномерным кодом определенной длины 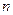 над алфавитом
над алфавитом 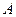 , то длину
, то длину 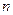 нужно выбрать так, чтобы число всех разных комбинаций было меньше чем
нужно выбрать так, чтобы число всех разных комбинаций было меньше чем  . Наибольшее число, при котором это возможно, или мера разнообразия множества состояний системы задается формулой Р.Хартли:
. Наибольшее число, при котором это возможно, или мера разнообразия множества состояний системы задается формулой Р.Хартли:  (1.5)
(1.5)
где  - коэффициент пропорциональности (масштабирования, зависимо от выбранной длины измерения),
- коэффициент пропорциональности (масштабирования, зависимо от выбранной длины измерения),  - основа системы меры,
- основа системы меры,  - количество информации, которую дает появление одного из
- количество информации, которую дает появление одного из  равновозможных состояний системы.
равновозможных состояний системы.
Поскольку в информационных процессах наиболее широко используется двоичная система счисления, то из практических соображений выбирают 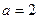 . Формулу Хартли рассматривают в виде:
. Формулу Хартли рассматривают в виде:
 (1.6)
(1.6)
где  - количество равновозможных состояний системы,
- количество равновозможных состояний системы,  - количество информации в битах. Отметим, что бит в данном случае имеет другое толкование, чем при техническом (алфавитном) подходе при оценивании информации. Бит – это количество информации, которая поступает от системы, что имеет два разных, одинаково возможных для реализации состояний.
- количество информации в битах. Отметим, что бит в данном случае имеет другое толкование, чем при техническом (алфавитном) подходе при оценивании информации. Бит – это количество информации, которая поступает от системы, что имеет два разных, одинаково возможных для реализации состояний.
 .
.
Следовательно, тут бит не является наименьшей единицей измерения информации.
 |
Дата добавления: 2015-09-11; просмотров: 1422;
