Контрольные задания. 1. Что называется дифракцией света?

1. Что называется дифракцией света?

2. В чем состоит сущность метода зон Френеля?

3. Выведите формулы для определения радиусов и площадей зон Френеля.

4. Зависит ли площадь зон Френеля от номера зоны?

5. Как зависит интенсивность света в точке P от числа открытых зон Френеля?

6. Как меняется дифракционная картина, если при данных r и R увеличивать расстояние от отверстия до экрана?

7. Каково соотношение между интенсивностями света в точке P в случаях, когда отверстие открывает одну зону Френеля и при полностью открытом волновом фронте?

Список литературы

1. Савельев И.В. Курс физики. М.: Наука, 1989.-Т.3.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2003. – 720 с.

3. Ландсберг Г.С. Оптика. Учебное пособие: Для вузов. – 6-е изд., стереотип. – М.: Физматлит, 2003. – 848 с.

Работа 303

Изучение явления дифракции света в параллельных лучах (дифракция Фраунгофера)

Цель работы: изучение дифракции света при падении плоской когерентной монохроматической волны на щель в непрозрачном экране и нить; использование дифракционных явлений для определения длины волны света и неконтактного измерения толщины нити.

Приборы и принадлежности: источник света газовый (He-Ne) лазер, щель регулируемой ширины, нить, матовый экран с горизонтальной миллиметровой шкалой, линейка.

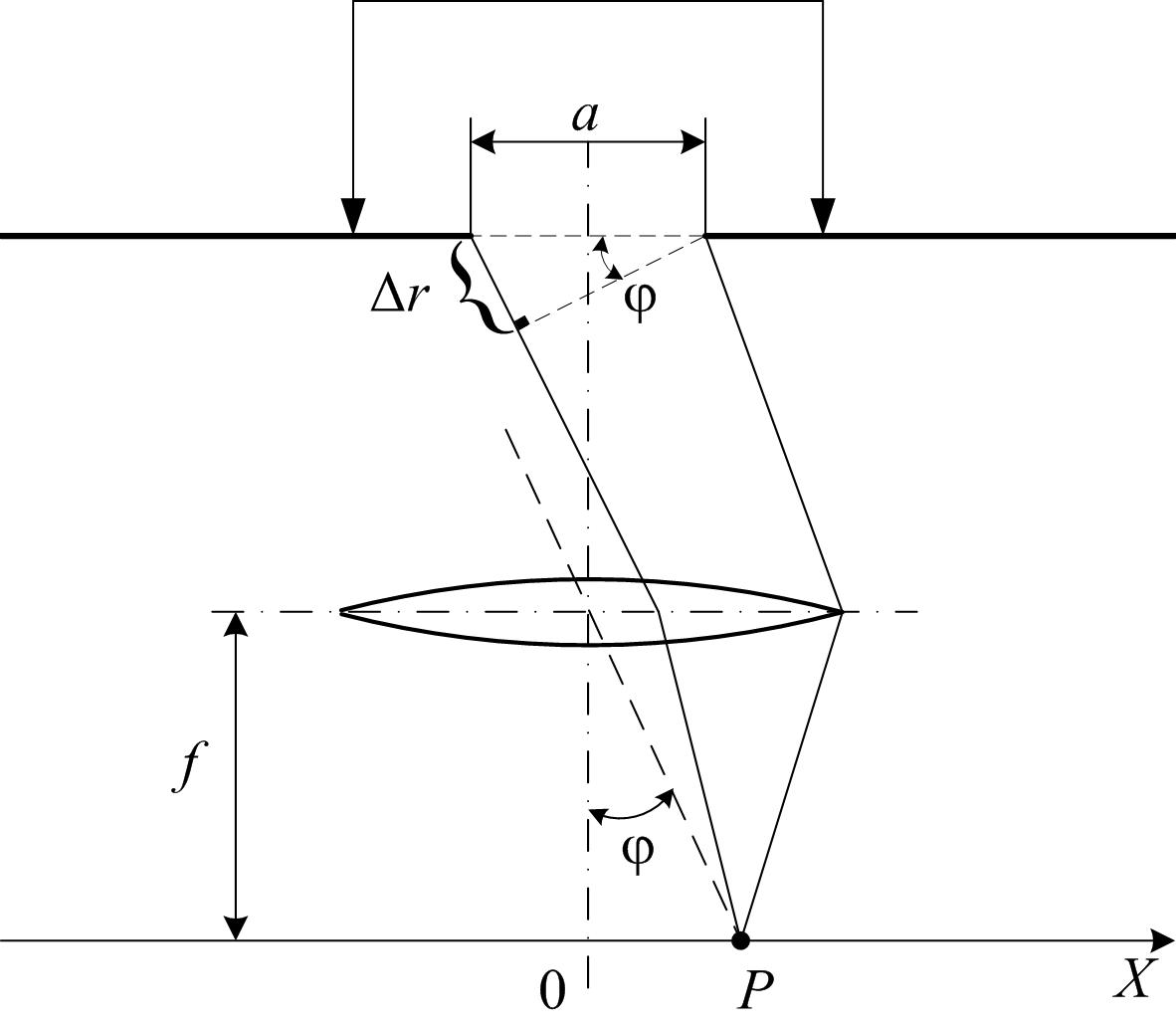
Рис. 1.

Рассмотрим дифракцию света (определение явления дифракции см. [2] при падении плоской когерентной монохроматической волны на длинную щель в непрозрачном экране (рис. 1). Пусть свет падает на щель нормально к ее поверхности, так что колебания в плоскости щели совершаются в одной фазе. Для того, чтобы наблюдать дифракцию Фраунгофера, точку наблюдения Р необходимо расположить на достаточно большом расстоянии, где лучи, идущие от краев щели в точку Р, будут практически параллельными. Это условие легко реализовать, поместив за щель собирающую линзу так, чтобы точка наблюдения Р находилась в фокальной плоскости линзы (линза собирает в фокальной плоскости в одной точке параллельные лучи).

Решим задачу о дифракции Фраунгофера на щели, используя метод графического сложения амплитуд. Для этого разобьем открытую часть волновой поверхности на узкие полоски одинаковой ширины а₀ параллельные краям щели. Колебания, возбуждаемые каждой такой плоскостью в точке наблюдения Р, имеют одинаковую амплитуду А₀ и отстают по фазе от предыдущего колебания на величину

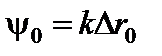, (1)

где k = 2p/l – волновое число;

λ – длина волны;

Dr₀ = а₀sinj – разность хода лучей, приходящих в точку Р от соседних полосок;

j – угол дифракции, определяющей направление на точку P.

Соответственно разность фаз между лучами, идущими в точку Р от краев щели, будет равна

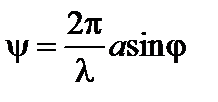, (2)

где а – ширина щели.

При выводе соотношений (1) и (2) учитывалось, что линза не вносит дополнительной разности хода лучей. Для определения результирующей амплитуды колебания удобно использовать векторные диаграммы. С этой целью амплитуде колебания, возбуждаемого m-й полоской в точке Р. ставится в соответствие вектор А_m, модуль которого равен A₀, а направление задается таким образом, чтобы угол между векторами А_т и А_т-1 отличался на y₀. Векторная диаграмма (рис. 2.) иллюстрирует сложение векторов А_m и позволяет найти результирующий вектор, модуль которого равен амплитуде A результирующего колебания в точке Р. При j = 0 разность фаз y₀ = y = 0.

Если y = p, колебания от краев щели находятся в противофазе. Соответственно векторы А_m располагаются вдоль полуокружности (см. рис. 2.) длиной L. Результирующая амплитуда при этом оказывается равной диаметру полуокружности и может быть найдена из равенства

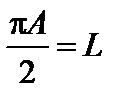, откуда .

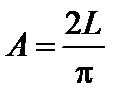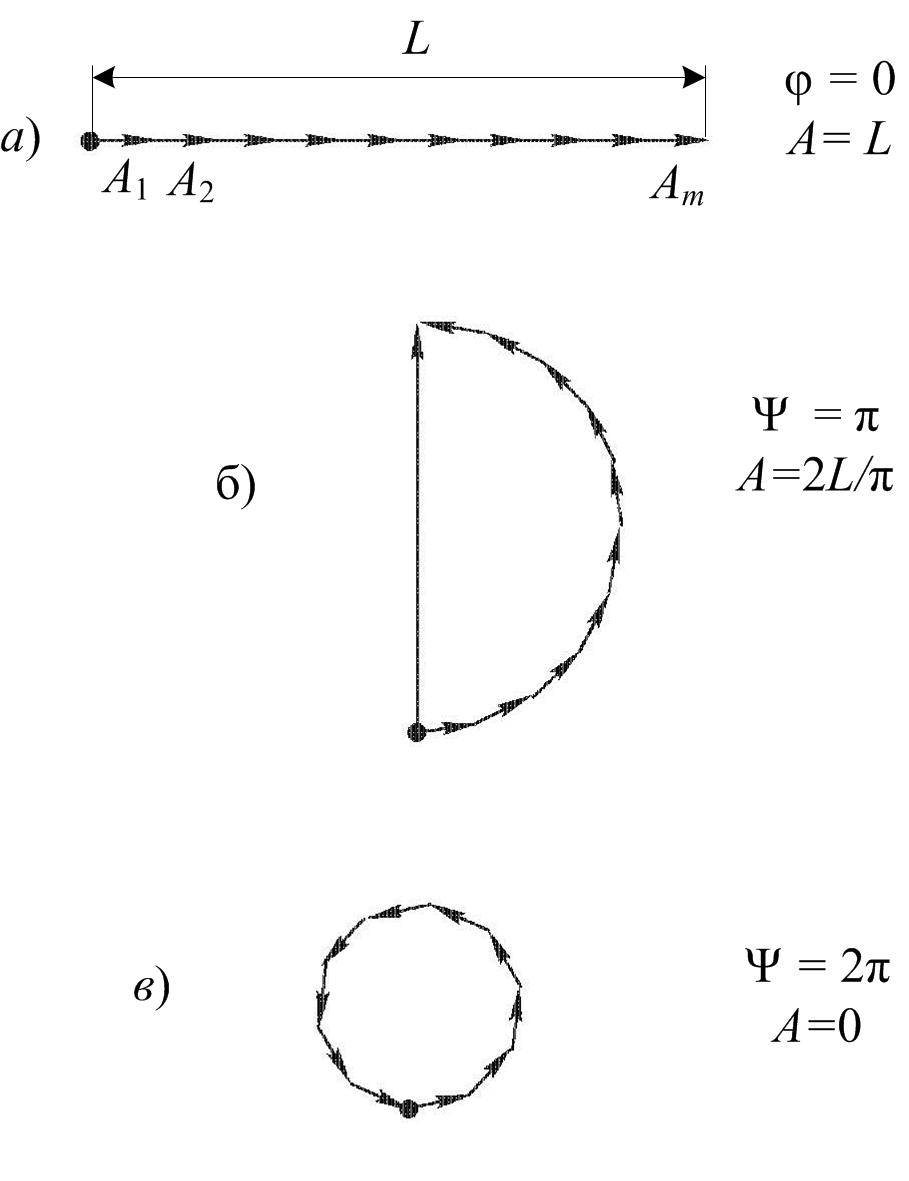
Рис. 2.

В случае y = 2p, (рис. 2.) векторы А_m располагаются вдоль окружности длиной L. Результирующая амплитуда равна нулю – получается первый минимум. Первый максимум получается при y = 3p,. Найдем его амплитуду.

,

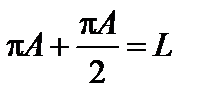следовательно:

.

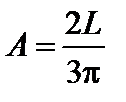Продолжая аналогичные построения, можно прийти к выводу, что дифракционная картина представляет собой чередование максимумов и минимумов интенсивности света, причем интенсивность n-го максимума ослабевает от центра дифракционной картины к её краям в следующем соотношении [3]:

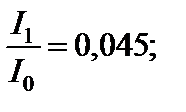
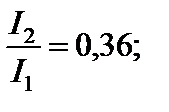
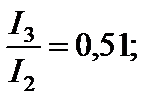
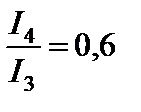и т. д.

Условие образования n-го минимума дифракционной картины Фраунгофера может быть записано в виде:

y = ±2np,

где n = 1, 2, 3, ….., или, с учетом выражения (2),

аsinj = ±nl.(3)

Как следует из рис. 1,

,

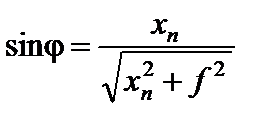где х_n – координата n-го минимума в плоскости наблюдения,

f – фокусное расстояние линзы.

При условии f >> х_n

,

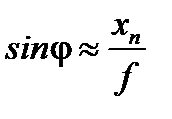следовательно, имеет место равенство

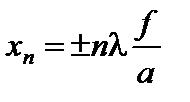. (4)

При переходе от n-го минимума к (n + 1-му) координата x точки Р изменяется на величину

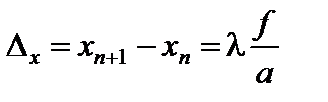. (5)

Расстояние ∆_x, таким образом, определяет ширину дифракционной полосы. Зная D_x, f и a, по формуле (5) можно определить длину волны света l, а при известных l, f и ∆_x – ширину щели a (или нити) [3].