Дисперсия постоянной равна нулю.
Доказательство. Пусть 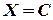 . По формуле (4.8) имеем
. По формуле (4.8) имеем
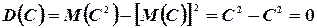
так как математическое ожидание постоянной есть эта постоянная:

2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
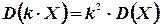 (4.9)
(4.9)
Доказательство. На основании соотношения (4.8), можно записать
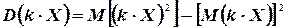
Так как
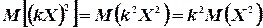
и
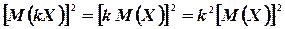
то
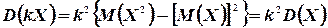
3°. Если 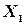 и
и 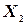 - независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий:
- независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий:
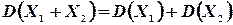 (4.10)
(4.10)
Доказательство. По формуле (4.8) имеем
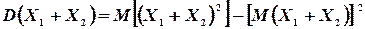
Но
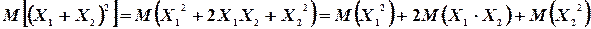
Так как 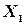 и
и 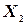 - независимые случайные величины, то
- независимые случайные величины, то
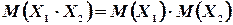
Следовательно
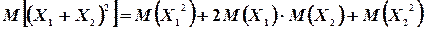
Далее,
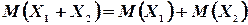
поэтому
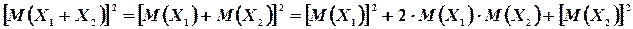
Таким образом
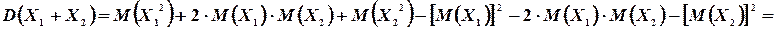
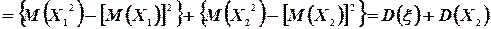
Следовательно
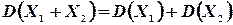
Замечание. Свойство 3° распространяется на любое конечное число попарно независимых случайных величин:
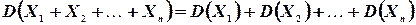
Средним квадратическим отклонением 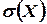 случайной величины
случайной величины 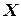 называется корень квадратный из ее дисперсии:
называется корень квадратный из ее дисперсии:
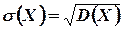 (4.11)
(4.11)
Среднее квадратическое отклонение 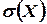 имеет ту же размерность, что и случайная величина
имеет ту же размерность, что и случайная величина 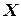 .
.
Пример 4.1. Случайная величина 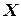 - число очков, выпадающих при однократном бросании игральной кости. Определить: математическое ожидание, дисперсию и средне квадратическое отклонение.
- число очков, выпадающих при однократном бросании игральной кости. Определить: математическое ожидание, дисперсию и средне квадратическое отклонение.
Решение: Используя формулы (4.1), (4.6) и (4.11) соответственно получим
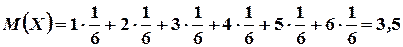
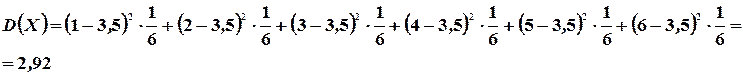
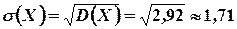
Дата добавления: 2015-09-11; просмотров: 1063;
