Формула полной вероятности.
Пусть событие A может произойти только вместе с одним из попарно несовместных событий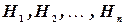 
, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий 
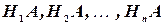: либо 
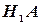, либо 
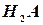, либо 
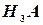и т.д. Следовательно,
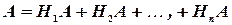
Применяя аксиому сложения вероятностей, имеем
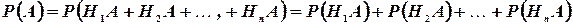
Но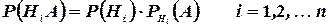 
,
поэтому
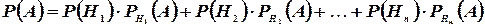(1.12)
Эта формула называется формулой полной вероятности. События 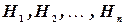часто называют «гипотезами».
Пример 1.10. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах. C 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?
Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а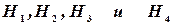 
— гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны:
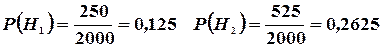
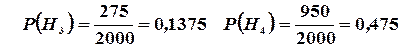
Далее, из условия задачи следует, что
Используя формулу полной вероятности (11), имеем
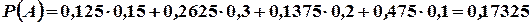
7. Формула Бейеса.
Предположим, что будет производится некоторый опыт, причем об условиях его проведения можно высказать n (единственно) возможных и несовместных гипотез 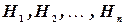, имеющих вероятности 
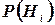. Пусть в результате проведения этого опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы 
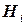, то 
.
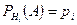
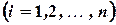Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей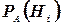 
.
На основании соотношений (5) и (6) имеем
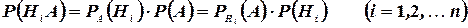
Откуда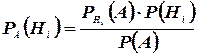 
.
Но по формуле полной вероятности
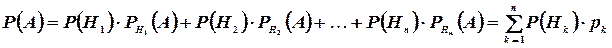
Поэтому
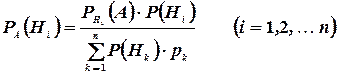(1.13)
Формула (13) называется формулой Бейеса (Т. Бейес (ум. 1763) - английский математик.).
Пример 1.11. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?
Решение: Пусть A — событие, состоящее в том, что взятый подшипник нестандартный, а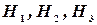 
- гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют
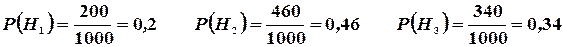
Из условия задачи следует, что
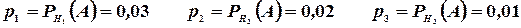
Найдем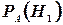 
, т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем
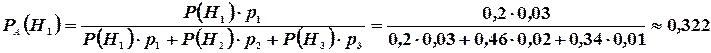
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.
Пример 1.12. Команда стрелков состоит из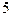 
человек. 
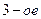из ни попадают в цель с вероятностью 
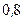, а двое - с вероятностью 
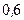. Наудачу из команды берется стрелок и производит выстрел.
а). Какова вероятность того, что стрелок попадет.
б). Если стрелок попал в цель, то какова вероятность, что это один из трех (один из двух).
Дата добавления: 2015-09-11; просмотров: 1335;