Условная вероятность. Теорема умножения вероятностей.
Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В.
Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
| 3-й исход | надпись | герб |
| 4-й исход | надпись | надпись |
Таким образом, 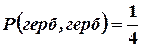 .
.
Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях 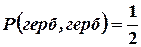 . Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.
. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать 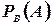 . Таким образом,
. Таким образом, 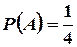 ;
; 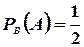 .
.
Теорема 3 (теорема умножения). Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
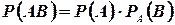 (1.5)
(1.5)
Доказательство. Докажем справедливость соотношения (5), опираясь на классическое определение вероятности. Пусть возможные исходы 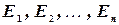 данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют
данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют 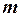 исходов, и пусть из этих
исходов, и пусть из этих 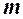 исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и Bблагоприятствуют L из
исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и Bблагоприятствуют L из 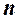 возможных результатов испытания. Это дает
возможных результатов испытания. Это дает 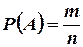 ,
, 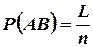 ,
, 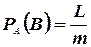 .
.
Таким образом, 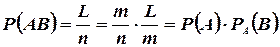 . Поменяв местами A и B, аналогично получим:
. Поменяв местами A и B, аналогично получим:
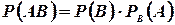 (1.6)
(1.6)
Из формул (5) и (6) имеем
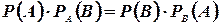 (1.7)
(1.7)
Теорема умножения легко обобщается на любое, конечное число событий. Так, например, в случае трех событий 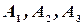 имеем (Событие
имеем (Событие 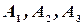 можно представить как совмещение двух событий: события
можно представить как совмещение двух событий: события 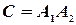 и события
и события 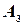 )
)
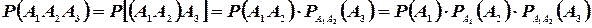
В общем случае
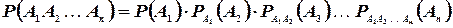 (1.8)
(1.8)
Дата добавления: 2015-09-11; просмотров: 882;
