Для обеспечения сопоставимости показатели приводятся к единой базе.
В первую очередьнейтрализуют влияние на величины анализируемых показателей ценового фактора, изменяющегося под воздействием инфляции, для чего сравниваемые показатели выражают в одних и тех же ценах: ценах отчетного периода или в ценах одного из предыдущих периодов. Для пересчета используют индекс цен – один из индивидуальных индексов, характеризующий изменение цены определенной продукции в текущем (отчетном, анализируемом) периоде по сравнению с базисным (прошлым) периодом. Чтобы определить величину стоимостного показателя анализируемого периода в ценах базисного, необходимо его величину разделить на произведение индексов цен за ряд предыдущих периодов и если наоборот, то умножить на произведение индексов цен.
Показатели могут быть несопоставимы из-за объемного фактора. Чтобы сравнить сумму затрат на производство продукции в базисном периоде  с затратами в отчетном периоде
с затратами в отчетном периоде 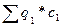 , необходимо нейтрализовать влияние объемного фактора. Для этого сумму затрат базисного года пересчитывают на фактический объем производства продукции отчетного года
, необходимо нейтрализовать влияние объемного фактора. Для этого сумму затрат базисного года пересчитывают на фактический объем производства продукции отчетного года 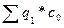 Σ и после этого сравнить с фактической суммой затрат:
Σ и после этого сравнить с фактической суммой затрат: 
Для нейтрализации воздействия качественного фактора обычно объем полученной продукции приводят к стандартному качеству, соответственно уменьшая или увеличивая ее количество.
Чтобы привести сравниваемые показатели к одинаковой структуре, необходимо физический объем производства продукции пересчитать на структуру базисного периода.
Сопоставимость показателей в ряде случаев может быть обеспечена применением вместо абсолютных величин средних или относительных величин. Например, несравнимы такие абсолютные показатели как объем производства товарной продукции и прибыль от продаж для различных предприятий, если не учесть производственную базу (активы) предприятия. Для обеспечения сопоставимости в этом случае можно вместо абсолютных показателей рассчитать относительные, к примеру, относительные показатели: «объем производства на одного работника» и «сумма прибыли на рубль активов».
Большое значение в вопросе обеспечения сопоставимости показателей имеет соответствие методик расчета сравниваемых показателей. Например, рентабельность продукции можно рассчитать по валовой прибыли, по прибыли от продаж, чистой прибыли; по производственной себестоимости продукции или по полной себестоимости. Нужно иметь в виду, что несоответствие методик может не только исказить результаты сравнения, но и вообще изменить их смысл.
Для обеспечения сопоставимости добиваются также однородности сравниваемых составляющих. Например, нельзя сравнивать показатели цеха с показателями предприятия в целом, себестоимость товарной и себестоимость реализованной продукции, валовую прибыль и чистую прибыль и т.д.
Известно. что первичными показателями, характеризующими объект экономического анализа, являются абсолютные показатели. Экономические показатели в форме абсолютных величин характеризуют абсолютные размеры анализируемых процессов и явлений: стоимость, их массу, объем, площадь и т.д. безотносительно к размеру других явлений. Абсолютные экономические показатели всегда являются именованными числами, они выражаются в натуральных, стоимостных или трудовых единицах измерения. Наибольшее значение имеют стоимостные показатели, дающие денежную оценку экономическим явлениям и процессам. Они наглядно дают оценку исследуемого явления, но подвержены влиянию инфляции, характеризуют размер явления, но не дают оценку эффективности использования ресурса.
Для экономического анализа характерно использованиеотносительных величинвторичных, отражающих результат от деления одного абсолютного показателя на другой. Все используемые в анализе относительные показатели,подразделяют напоказатели: динамики; структуры; координации; интенсивности; сравнения; эффективности.
Относительный показатель динамики представляет собой отношение уровня исследуемого процесса или явления за анализируемый (отчетный) период времени к уровню этого же процесса или явления в прошлом. Его величина показывает, во сколько раз текущий (отчетный) уровень превышает предшествующий (базисный) или какую долю последнего составляет. Его называют обычно темпом роста.
Пример 3.1.:
Определить темпы роста и темпы прироста, если на предприятии выработано в предыдущем году 485 тонн, в отчетном 488 тонн продукции.
Темп роста, как отношение последующего года к предыдущему. 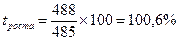
Темп прироста, то есть относительного прироста:  .
.
Особое значение имеют базисные и цепныеиндексы, которые служат для оценки темпов изменения показателей во времени. Индекс, который характеризует изменение (рост или снижение) уровня показателя в течении какого-либо периода и отражает отношение исследуемого показателя к базовому (или плановому). называется базисным индексом. Базисный индекс между анализируемым уровнем ряда и уровнем, принятым на базу определяется по формуле:
Убазис. = Уn – Уб . (3.1)
Цепной индекс рассчитывается в результате сравнения показателей последующего периода с предыдущим. рассматривает изменение – разность между последующим и предыдущим уровнем.
Уцепн. = Уn – Уn-1 (3.2)
Интегральный индекс – произведение нескольких частных показателей, используемых для комплексной характеристики уровня эффективности процессов и явлений.
Пример 3.2:
Таблица 3.1. Определить индекс производства продукции по следующим данным:
| Год | Объем производства, тыс.т | Цепной индекс |
| 1,0 | ||
| 1,06 | ||
| 1,03 | ||
| 1,029 |
Приведенные данные показывают, что при постоянном увеличении объема выпускаемой продукции предприятие в 2007 и 2006 г. снизило темпы роста производства по сравнению с 2005 г.
В этом случае необходимо более детальное исследование причин изменения показателей.
Относительный показатель структурырассчитывается как отношение показателя, характеризующего часть совокупности к показателю по всей совокупности в целом (в долях единицы или процентах).
Относительные показатели координациихарактеризуют соотношение отдельных частей и целого между собой. При этом, в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической точки зрения. В результате получают, сколько единиц каждой структурной части приходится на 1единицу (иногда на 100, 1000 и т.д. единиц) базисной структурной части.
Относительный показатель интенсивности характеризует степень распространения изучаемого процесса или явления в присущей ему среде. Он исчисляется как отношение показателя, характеризующего явление «А» к показателю, характеризующему среду распространения явления «А». Этот показатель исчисляется, когда абсолютная величина оказывается недостаточной для формулирования обоснованных выводов о масштабах экономического явления, его размерах и т.п.
Относительный показатель сравнения представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты ( подразделения, предприятия и т.п.):
Относительные величины эффективности – это соотношение эффекта с ресурсами или затратами, например прибыль на рубль затрат, на рубль выручки, на одного рабочего.
Относительные показатели, применяемые при исследовании финансово-хозяйственной деятельности предприятия называют финансовыми коэффициентами. Они характеризуют соотношения между различными статьями бухгалтерской (финансовой) отчетности. Наиболее распространенными для анализа являются пять групп относительных финансовые показателей – финансовых коэффициентов: коэффициенты платежеспособности и ликвидности; финансовой устойчивости; деловой активности; рентабельности; рыночной активности (см. темы 7,8,9).
Средние величины используются в экономическом анализе для обобщенной количественной характеристики массовых, качественно однородных экономических совокупностей однородных явлений, т.е. одним числом характеризуют всю совокупность объектов (средняя стоимость основных производственных фондов, среднесписочная численность работающих, средняя заработная плата и т.д.). Средняя величина - это аналитический показатель «середины» или «центра» исследуемых данных.
Различают разновидности средних величин: степенные средние (средняя арифметическая; средняя гармоническая; средняя геометрическая; средняя квадратическая, кубическая и т.д.) и структурные средние ( мода; медиана).
Средняя арифметическая – самый простой вид средней, которая определяется путем деления суммы значений варьируемого признака на число значений.
Дата добавления: 2015-09-11; просмотров: 1057;
