Теория фильтрационной консолидации.
Опыт строительства сооружений на глинистых грунтах показывает, что осадки сооружений происходят не мгновенно, а развиваются длительное время: десятки, а иногда и сотни лет. Замедление во времени деформаций водонасыщенных глинистых грунтов связано с процессом фильтрационной консолидации, под которым понимают уплотнение грунта за счет отжатия воды из его пор. Чем выше водопроницаемость грунта, тем быстрее отжимается вода из его пор и тем быстрее протекает осадка основания сооружения.
Решение задачи линейной фильтрационной консолидации основано на допущениях:
1) рассматриваются полностью водонасыщенные грунты со свободной несжимаемой водой в порах грунта;
2) уплотнение грунта может происходить только за счет выдавливания воды, т.е. уменьшения объема пор скелета грунта;
3) скелет грунта принимается линейно-деформируемым, напряжения в котором мгновенно вызывают его деформации;
4) грунт не обладает структурностью, и внешнее давление, прикладываемое к нему, в первый момент времени полностью передается на воду;
5) фильтрация воды в порах грунта полностью подчиняется закону Дарси.
Согласно допущению 2 увеличение расхода воды q для элементарного слоя dz, расположенного на глубине z, должно быть равно уменьшению пористости грунта n в единицу времени t согласно условию:
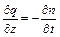 .
.
Выполнив необходимые преобразования левой и правой частей этого уравнения, получают:
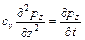 ;
;
где сv – коэффициент консолидации грунта, м2/сут или м2/год,
принимается равным:
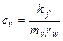 .
.
pz - давление, передающееся на твердые частицы (эффективное).
mv – коэффициент относительной сжимаемости;
kf – коэффициент фильтрации.
Это и есть уравнение одномерной теории фильтрационной консолидации (уплотнения) грунтовой массы. Решение этого уравнения находят путем применения рядов Фурье и удовлетворения начальным граничным условиям.
Для практики необходимо часто иметь осадку для любого промежуточного времени с момента начала загружения, т.е. st. Для определения этой величины вводится понятие степени консолидации. Если принять степень консолидации при полной стабилизированной осадке за единицу, а за время t– u, то
u = st / s.
Математически это выражается следующим образом:
 ;
;
где А – площадь эпюры давлений при полной стабилизированной осадке
(А = ph).
Подставляя значение pz, затем интегрируя и ограничиваясь первым членом ряда, получается:
 , где
, где 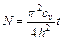 .
.
С учетом зависимости u=st/s и подставляя выражение для осадки слоя, получим для основного случая (равномерного распределения уплотняющих давлений по глубине) осадку для любого времени:
 .
.
Дата добавления: 2015-09-11; просмотров: 2889;
