Распределение напряжений от полосовой нагрузки (плоская задача).

Условия плоской задачи будут иметь место в случае, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они будут или равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок и др. Для этих сооружений в любом месте, за исключением лишь краевых участков, распределение напряжений в любом проверенном сечении будет таким же, как и в других соседних, при условии, что в направлении, перпендикулярном рассматриваемой плоскости, нагрузка не меняется.

Наиболее часто применяемые на практике решения получены путем использования формулы для напряжений в линейно-деформируемом массиве от погонной нагрузки.

Выражения для составляющих напряжений σ_z, σ_y, τ будут иметь вид:

;

;

.

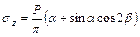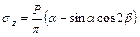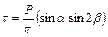Приведенные выражения позволяют легко составить таблицу коэффициентов влияния для вычисления составляющих напряжений, введя обозначения:

; ; .

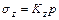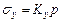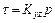Значения коэффициентов К_z, K_y, K_yz приведены в таблицах учебников в зависимости от координат z/b и y/b.

На основе табличных данных легко построить эпюры распределения напряжений по горизонтальным и вертикальным сечениям массива грунта (рис. 17).

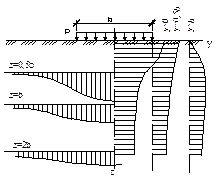
Рис.17. Эпюры распределения сжимающих напряжений по