Политропный процесс. а) Любой произвольный процесс можно описать выражением , подбирая соответствующее значение п

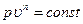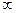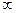а) Любой произвольный процесс можно описать выражением , подбирая соответствующее значение п. Процесс, описываемый этим уравнением, называется политропным. Показатель политропы n может принимать любое значение в пределах от - до + . Все рассмотренные выше процессы входят в политропный процесс как частные случаи.

При ;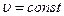

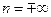при ;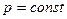

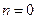при ;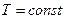

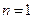при .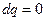

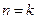Используя уравнение политропы и уравнение Клапейрона, получим выражения, устанавливающие взаимосвязь между p, 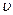и T в политропном процессе:

;

;

.

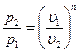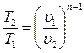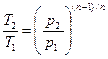б) ;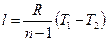

;

;

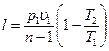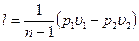г) ;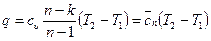

д)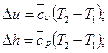

е) .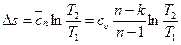

Графики политропных процессов

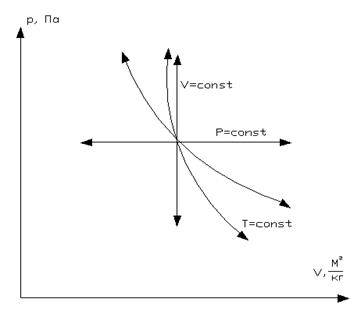
Рис. 1.18 – Политропный процесс в 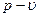координатах

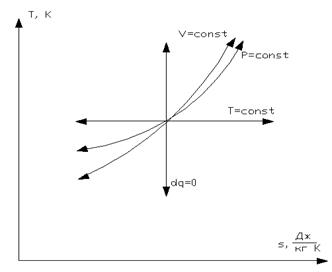
Рисунок 1.19 – Политропный процесс в T-s координатах

Процессы в координатах p- 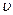, идущие вправо от исходного состояния (расположенные правее изохоры) протекают с совершением работы и называются процессами расширения, для них работа l >0.

Процессы в координатах p- 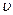, идущие влево от исходного состояния (расположенные левее изохоры) протекают с затратой работы внешних сил и называются процессами сжатия, для них работа l <0.

В координатах 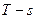все процессы идущие вправо от исходного состояния (расположенные правее адиабаты) протекают с подводом теплоты, для них теплота процесса q > 0. Процессы, направленные влево от исходного состояния (расположенные левее адиабаты) протекают с отбором теплоты, для них теплота процесса q< 0.