Основные термодинамические процессы в газах
Различают следующие основные термодинамические процессы в идеальных газах:
1. Изохорный процесс;
2. Изобарный процесс;
3. Изотермический процесс;
4. Адиабатный процесс;
5. Политропный процесс.
При исследовании термодинамического процесса в общем случае определяют такие его параметры:
а) Уравнение процесса.
б) Графики процессов в координатах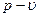 
и T-s.
в) Работу l, совершаемую 1 кг тела за процесс.
г) Теплоту процесса q.
д) Изменение внутренней энергии Δu и энтальпии Δh.
е) Изменение энтропии Δs.
1. Изохорный процесс (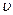 
=const)
Уравнение процесса получаем из уравнения Клапейрона:
.
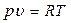Разделяя переменные и постоянные величины, получим:
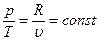или 
.
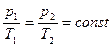а) Изохорному процессу соответствует закон Шарля:
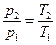
- давление газа в изохорном процессе прямо пропорционально его абсолютной температуре.
б) Графики изохорного процесса в координатах 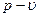и T-s представлены на рис. 1.13. и на рис. 1.14.
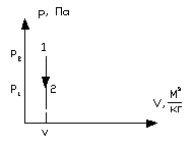
Рисунок 1.13 – Изохорный процесс в координатах
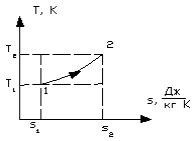
Рисунок 1.14 – Изохорный процесс в T-s координатах
в) l=0;
г)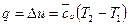 
;
д)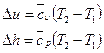 
, так как 
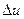и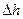 
есть функции состояния и не зависят от характера процесса, то формулы для определения 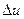и 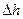будут одинаковы для всех процессов.
е) Изменение энтропии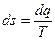 
, а за процесс 
;
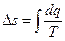Используя первый закон термодинамики, получим:
,
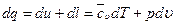где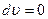 
, тогда 
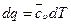, следовательно:
.
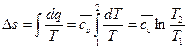3. Изобарный процесс (p= const)
а) Уравнение процесса получаем из уравнения Клапейрона:
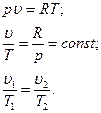
Уравнение изобарного процесса:
.
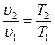Это закон Гей-Люссака (1802 г.) - удельный объем газа в изобарном процессе прямо пропорционально его абсолютной температуре.
б) Графики изобарного процесса в координатах 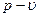и T-s
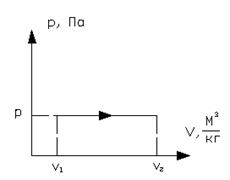
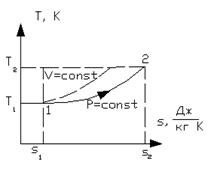
Рисунок 1.15 – Изобарный процесс в 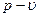и T-s координатах
в)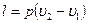 
;
или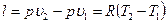 
;
г)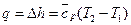 
;
д)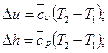 
е)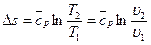 
.
4. Изотермический процесс (Т=const)
а) Уравнение процесса получаем из уравнения уравнение Клапейрона:
.
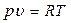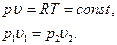
Получили закон Бойля-Мариотта – в изотермическом процессе давление и удельный объем обратнопропорциональны друг другу:
.
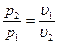б) Графики изотермического процесса в координатах 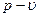и T-s
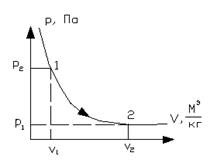
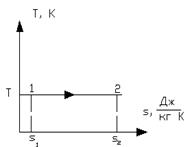
Рисунок 1.16 – Изотермический процесс в 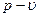и T-s координатах
в)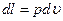 
;
;
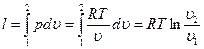г)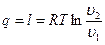 
;
д)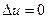 
;
;
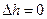е)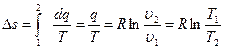 
.
5. Адиабатный процесс
а) Адиабатный процесс протекает без теплообмена с окружающей средой (либо так быстро, что теплообменом можно пренебречь)
.
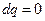Уравнение адиабатного процесса
,
,
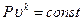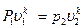где k – показатель адиабаты, зависит от строения вещества.
Показатель адиабаты k может быть определен как отношение изобарной теплоемкости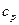 
и изохорной теплоемкости 
:
,
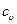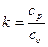где k=1,66 – для одноатомных (инертных) газов,
k=1,40 – для двухатомных газов,
k=1,33 – для трехатомных газов.
Уравнение адиабатного процесса также может быть представлено в виде:
;
;
.
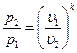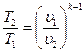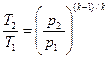б) Графики адиабатного процесса в координатах 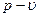и T-s
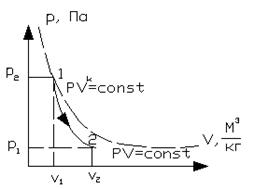
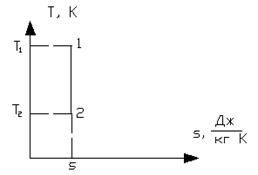
Рисунок 1.17 - Адиабатный процесс в 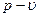и T-s координатах
в)
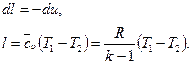
Используя выражения для показателя адиабаты k и уравнение Майера, получим выражение для определения :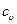
.
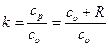
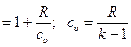Тогда:
.
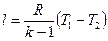г)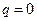 
;
д)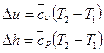 
;
е) ,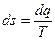 
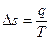. Поскольку 
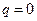, то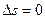 
и s=const.
Дата добавления: 2015-09-11; просмотров: 2924;