Переходные процессы заряда и разряда емкостного элемента в цепи с источником постоянной ЭДС.

А. Зарядка емкостного элемента от источника постоянной ЭДС через резистивный элемент. Переходный процесс в цепи на рис. 5 описыва­ется неоднородным дифференциальным уравнением на основе второго закона Кирхгофа, закона Ома и = ri и соотношения между током за­рядки и напряжением в емкостном элементе i=Cdu_c/dt, т. е.

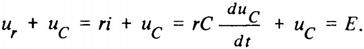(19)

Общее решение уравнения (19) представляет собой сумму двух составляющих:

u_С=u_Су+u_Сcв.

Первая составляющая соответствует установившемуся режиму

u_Су=Е,

так как зарядка емкостного элемен­та закончится, когда напряжение u_с будет равно напряжению источника ЭДС.

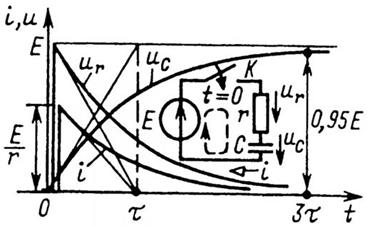
Рис. 5

Вторая составляющая соответствует свободному процессу, т. е. ре­шению однородного дифференциального уравнения первого порядка

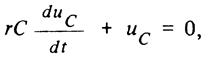
и равна

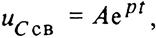(20)

где р=- 1/rС — корень характеристического уравнения rСр+1=0.

Таким образом, общее решение будет иметь вид

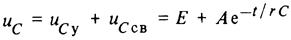(21)

Для определения значения постоянной А в (21) обратимся к за­кону коммутации для емкостного элемента. Будем считать, что до замыкания ключа, т. е. в момент времени t = 0_, емкостный эле­мент не был заряжен. Поэтому

и_с( 0_) = 0 = и_с (0₊) =Е + А, откуда А = -Е.

Подставив значение постоянной А в (21), найдем напряжение на емкостном элементе во время зарядки (рис. 5):

и_с =E(1-е^-t/т), (22)

где τ = rС имеет размерность времени (Ом • Ф = Ом • А • с/В =с) и на­зывается постоянной времени цепи. Она, как и постоянная времени цепи на рис. 4,а определяет скорость переходного процесса.

Зависимость от времени напряжения на емкостном элементе [см. (22)] определяет зависимости от времени зарядного тока и напряже­ния на резистивном элементе (рис. 5):

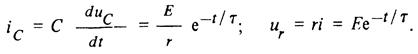
Заметим, что в первый момент после замыкания ключа, т. е. при t = 0₊ , ток в цепи i(0₊) =Е/r емкостный элемент в этот момент времени как бы коротко замкнут (напряжение на нем равно нулю). Поэтому при малом значении сопротивления r в цепи может наблю­даться значительный скачок тока.

При 0 ≤ t ≤ τ скорость изменения напряжения на емкостном элементе можно приближенно считать постоянной:

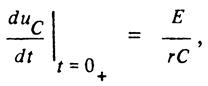
а напряжение

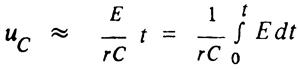
- пропорциональным интегралу напряжения источника ЭДС Е.

Если на входе цепи действует источник изменяющейся ЭДС е, то может оказаться, что для моментов времени переходного процесса, в которые и_r<<и_с, приближенно и_с ≈ е, a u_r = ri = rС du_C/dt≈ rCde/dt пропорционально скорости изменения напряжения источ­ника. Следовательно, цепь с последовательным соединением резистивного и емкостного элементов, так же как и цепь с последовательным соединением резистивного и индуктивного элементов, рассмотренную выше, при определенных условиях можно рассматривать и как ин­тегрирующую, и как дифференцирующую.

В большинстве случаев процесс зарядки можно считать практически закончившимся через интервал времени, равный 3τ. Этот интервал вре­мени может быть достаточно большим (чем больше r и С, тем боль­ше и τ), что широко используется, например, в реле времени — устрой­ствах, срабатывающих по истечении определенного времени.

Б. Разрядка емкостного элемента через резистивный элемент. В элект­рическом поле заряженного емкостного элемента сосредоточена энер­гия, за счет которой емкостный элемент в течение неко­торого времени сам может служить источником энергии. После под­ключения емкостного элемента, предварительно заряженного до напряжения и_C = Е, к резистивному элементу с сопротивлением r (рис. 6, а) ток в цепи будет обусловлен изменением заряда q емкост­ного элемента:

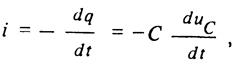(23)

где знак минус указывает, что ток i - это ток разрядки в контуре це­пи, обозначенном на рисунке штри­ховой линией, направленный навстре­чу напряжению на емкостном элементе.

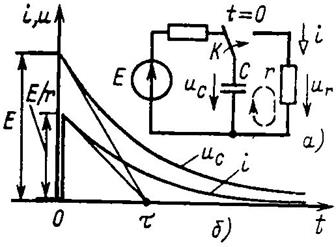
Рис. 6

Составим дифференциальное уравнение переходного процесса в контуре цепи, обозначенном на рис. 6, а штриховой линией, на основе второго закона Кирхгофа, закона Ома и соотношения (23):

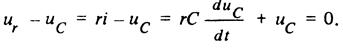(24)

Так как в цепи разрядки емкостного элемента нет источника ЭДС, то дифференциальное уравнение (24) однородное и его общее ре­шение состоит только из свободной составляющей:

u_с=u_с =Ae^-t/(rC). (25)

Для определения постоянной А в (25) обратимся к закону комму­тации для емкостного элемента (4). Так как до коммутации, т. е. и в момент времени t = 0_ , емкостный элемент был заряжен до на­пряжения источника, то

u_с(0_)=Е=u_с(0₊)=А.

Подставив значение постоянной А в (25), получим закон изме­нения напряжения при разрядке емкостного элемента (рис. 6, б):

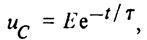
где τ = rС — постоянная времени цепи.

Разрядный ток найдем по (23):

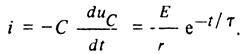
Ток разрядки скачком изменяется от нуля до значения i(0₊)= -Е/r, а затем убывает по экспоненциальному закону (рис. 6, б).