Мгновенные, средние и действующие значения

Ряд Фурье содержит мгновенные значения синусоидальных величин

но не сложно получить действующие и средние значения.

По определению, квадрат действующего значения тока I выражают через мгновенное значение тока i следующим образом:

Если ток

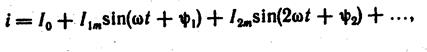
то

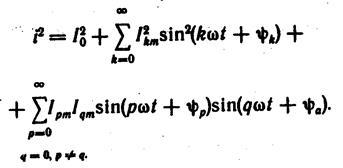
Но

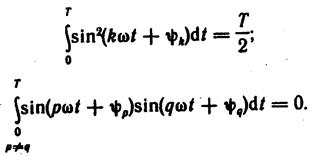
Поэтому

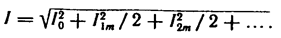
Или

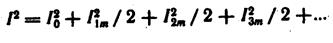
Так как амплитуда k-гармоники тока I_km в √2 раз больше дейст­вующего значения тока k-гармоники I_k то

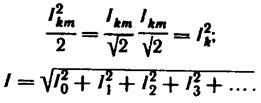
Следовательно, действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной состав­ляющей тока и действующих значений отдельных гармоник. От углов сдвига фаз ψ_k действующее значение тока не зависит.

Аналогично, действующее значение несинусоидального напря­жения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:

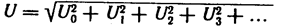
Среднее по модулю значение несинусоидальной функции.

Под средним по модулю значением функции понимают среднее значение модуля этой функции за период:

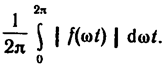
В отличие от действующего значения оно зависит от значений ψ_k.

Фильтры

В цепи периодического несинусоидального тока для различных гар­монических составляющих этого тока индуктивные сопротивления катушекkωL и емкостные сопротивления конденсаторов 1/kωС зави­сят от номера k гармонической составляющей.

На зависимости индуктивных и емкостных сопротивлений от частоты основан принцип работы электрических фильтров — устройств, при по­мощи которых гармонические составляющие токов и напряжений опре­деленной частоты или в пределах определенной полосы частот значи­тельно уменьшаются.

А. Сглаживающие фильтры. Сглаживающие фильтры служат для уменьшения процентного содержания на сопротивлении нагрузки гармо­нических составляющих выпрямленного напряжения или снижения про­центного содержания высших гармоник в кривой переменного напря­жения.

Рассмотрим работу простейшего сглаживающего фильтра (рис. 5), представляющего собой пассивный линейный четырехполюсник, к вы­ходным выводам которого подключен приемник с сопротивлением на­грузки г_2н. Коэффициент передачи напряжения фильт­ра, цепь которого вместе с приемником представляет собой цепь со сменянным соединением ветвей, равен

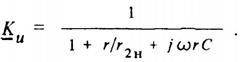
Соответствующая амплитудно-частотная характеристика фильтра

приведена на рис. 6. Чем выше частота гармоники напряжения на входе u_вх фильтра, тем меньше ее процентное содержание в напряже­нии на его выходе u_вых (рис. 7). Аналогичными свойствами обладает сглаживающий фильтр по схеме на рис. 8.

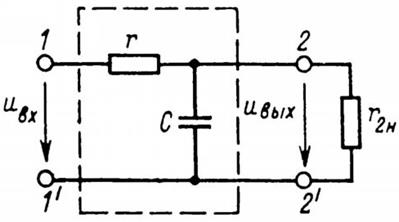
Рис. 5

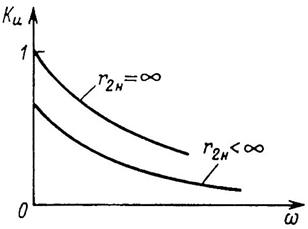
Рис. 6

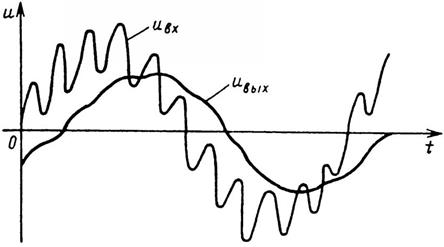
Рис. 7

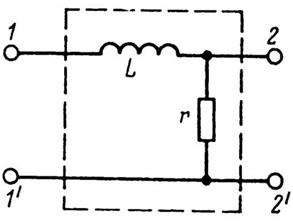
Рис. 8

Б. Резонансные фильтры. В резонансных фильтрах используются яв­ления резонансов напряжений и токов в электрических цепях для выделения или исключения в кривой напряжения на при­емнике определенной полосы частот. Соответствующие фильтры на­зываются полосовыми и заградительными.

На рис. 9, а приведена схема простейшего полосового фильтра на основе явления резонанса напряжений, а на рис. 9, б - его амплитуд­но-частотная характеристика, найденная по формуле:

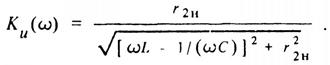
Ширина полосы частот Δω, выделяемая фильтром, на уровне тем меньше, чем больше добротность цепи .

В заградительном фильтре по схеме на рис. 10, а используется яв­ление резонанса токов. Его амплитудно-частотная характеристика

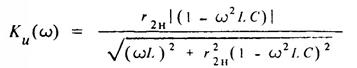
приведена на рис. 10,б.

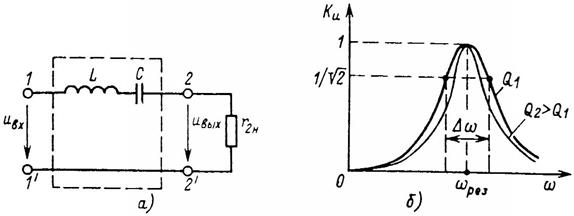
Рис. 9

Рис. 10

Комбинации явлений резонансов напряжений и токов в различных ветвях фильтра позволяют создавать полосовые и заградительные фильтры высокого качества.

В. Избирательные rC-фильтры. Фильтры, содержащие только рези­сторы и конденсаторы, называются rC-фильтрами. Отсутствие в них индуктивных элементов делает их привлекательными для реализации в виде интегральных микросхем. Примером полосового rС-фильтра может служить четырехполюсник (рис. 11, а), называемый мостом Вина, с коэффициентом передачи напряжения при разомкнутой цепи нагрузки

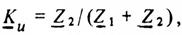
Амплитудно-частотная и фазочастотная характеристики моста Вина приведены на рис. 11, б. Максимальное значение амплитудно-частотной характеристики равно 1/3 и достигается при угловой частоте

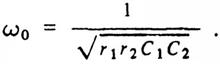
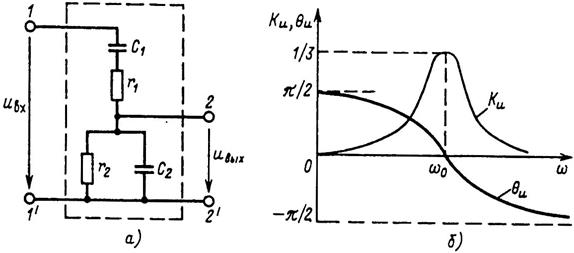
Рис. 11

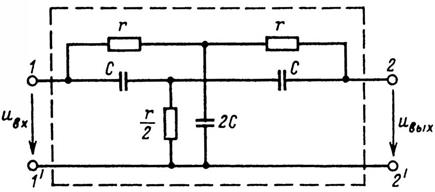
Рис. 12

При этом фазочастотная характеристика пересекает ось абсцисс, т.е. ϴ=0.

Заградительный rC-фильтр можно реализовать при помощи двой­ного Т-образного моста (рис. 12).

Возможны и другие схемотехнические решения избирательных rС-фильтров.

Подробно данную тему можно изучить в методическом пособии для практического занятия №4.